题目内容
9.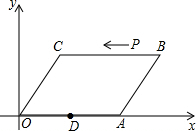 如图,在平面直角坐标系中,?OABC的顶点A,C的坐标分别为(10,0),(2,4),点D是OA的中点,点P在BC上由点B向点C运动,速度为2cm/s
如图,在平面直角坐标系中,?OABC的顶点A,C的坐标分别为(10,0),(2,4),点D是OA的中点,点P在BC上由点B向点C运动,速度为2cm/s(1)当点P运动多少秒时,四边形PCDA是平行四边形?并求此时点P的坐标;
(2)当△ODP是等腰三角形时,求点P的坐标.
分析 由四边形OABC是平行四边形,得到OA=BC,OA∥BC,于是得到OA=10,OE=AF=2,得到OD=AD=$\frac{1}{2}$OA=5,
(1)根据四边形PCDA是平行四边形,得到PC=AD,即10-2t=5,解方程即可得到结论;
(2)如图2,分三种情况①当PD=OD=5时,过P作PE⊥OA于E,则PE=4,得到DE=3,求出P1(8,4),②当PD=OP时,过P作PF⊥OA于F,则PF=4,OF=$\frac{5}{2}$,得到P3($\frac{5}{2}$,4);③当PO=OD=5时,过P作PG⊥OA于G,则PG=4,得到P2(3.4).
解答 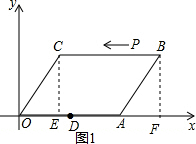 解:如图1,过C作CE⊥OA于E,过B作BF⊥OA于F,
解:如图1,过C作CE⊥OA于E,过B作BF⊥OA于F,
∵四边形OABC是平行四边形,
∴OA=BC,OA∥BC,
∵A,C的坐标分别为(10,0),(2,4),
∴OA=10,OE=AF=2,
∴BC=10,
∵点D是OA的中点,
∴OD=AD=$\frac{1}{2}$OA=5,
(1)设点P运动t秒时,四边形PCDA是平行四边形,
由题意得:PC=10-2t,
∵四边形PCDA是平行四边形,
∴PC=AD,即10-2t=5,
∴t=$\frac{5}{2}$,
∴当点P运动$\frac{5}{2}$秒时,四边形PCDA是平行四边形;
∴P($\frac{9}{2}$,4);
(2)如图2,①当PD=OD=5时,过P作PE⊥OA于E,
则PE=4,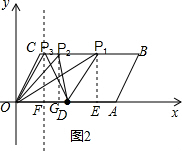
∴DE=3,
∴P1(8,4),
②当PD=OP时,过P作PF⊥OA于F,
则PF=4,OF=$\frac{5}{2}$,
∴P3($\frac{5}{2}$,4);
③当PO=OD=5时,过P作PG⊥OA于G,
则PG=4,
∴OG=3,
∴P2(3.4),
综上所述:当△ODP是等腰三角形时,点P的坐标为(8,4),($\frac{5}{2}$,4),(3.4).
点评 本题考查了平行四边形的性质,等腰三角形的性质,勾股定理,熟练掌握平行四边形的性质世界的推根据.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案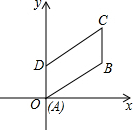 如图,在平行四边形ABCD中,∠DAB=60°,AB=2,AD=1,若点A在坐标原点,AB与x轴的夹角为30°,求平行四边形各顶点的坐标.
如图,在平行四边形ABCD中,∠DAB=60°,AB=2,AD=1,若点A在坐标原点,AB与x轴的夹角为30°,求平行四边形各顶点的坐标.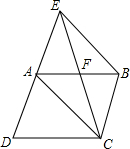 如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?
如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?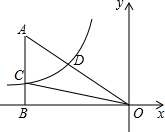 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18. 在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求:
在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求: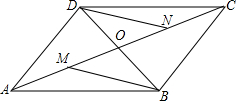 如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.
如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.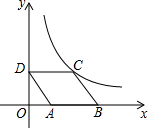 如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3).反比例函数的图象经过点C,则反比例函数的解析式是y=$\frac{12}{x}$(x≠0).
如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3).反比例函数的图象经过点C,则反比例函数的解析式是y=$\frac{12}{x}$(x≠0).