题目内容
6.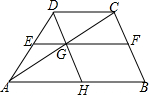 已知:如图,在?BCDH中,G是DH的中点,连接CG,CG与BH的延长线交于点A,连接AD,E是AD的中点,连接EG并延长交BC于点F,求证:GF=2EG.
已知:如图,在?BCDH中,G是DH的中点,连接CG,CG与BH的延长线交于点A,连接AD,E是AD的中点,连接EG并延长交BC于点F,求证:GF=2EG.
分析 直接利用三角形中位线定理得出EG$\stackrel{∥}{=}$$\frac{1}{2}$AH,进而得出△DGC≌△HGA(AAS),得出DC=AH,求出四边形DGFC是平行四边形,进而得出答案.
解答 证明:∵E是AD的中点,G是DH的中点,
∴EG是△DAH的平分线,
∴EG$\stackrel{∥}{=}$$\frac{1}{2}$AH,
∵四边形BCDH是平行四边形,
∴DC∥AB,DC=HB,
∴∠DCG=∠CAH,
在△DGC和△HGA中
$\left\{\begin{array}{l}{∠DCG=∠HAG}\\{∠CGD=∠AGH}\\{DG=GH}\end{array}\right.$,
∴△DGC≌△HGA(AAS),
∴DC=AH,
∵DC∥FG,DG∥FC,
∴四边形DGFC是平行四边形,
∴DC=FG,
∴EG$\stackrel{∥}{=}$$\frac{1}{2}$FG.
点评 此题主要考查了平行四边形的判定与性质以及全等三角形的判定与性质,得出△DGC≌△HGA(AAS)是解题关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
16.若式子$\frac{\sqrt{x-1}}{x+2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥1且x≠0 | B. | x>1 且x≠-2 | C. | x≥1 | D. | x≥1 且x≠-2 |
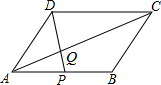 如图,在?ABCD中,点P在AB上,连结DP,交AC于点Q,当点P是AB的中点时,△ADQ的面积为1,则?ABCD的面积为( )
如图,在?ABCD中,点P在AB上,连结DP,交AC于点Q,当点P是AB的中点时,△ADQ的面积为1,则?ABCD的面积为( )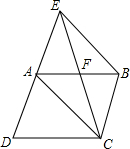 如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?
如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么? 在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求:
在矩形ABCD中,对角线AC与BD交于点O,∠AOB=60°,点E为AD边的中点,AC=8cm,AF⊥BD于点F.求: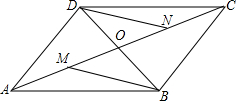 如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.
如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.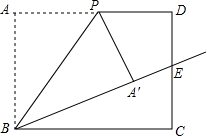 如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.