Question

1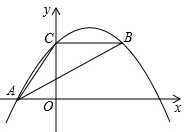．如图，抛物线y=ax²-4ax+2经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且OA=OC．
（1）求抛物线的对称轴；
（2）写出A，B，C三点的坐标并出求抛物线的解析式；
（3）探究：若点P是抛物线对称轴上且在x轴下方的动点，是否存在△PAB是等腰三角形．若存在，直接写出所有符合条件的点P坐标；若不存在，请说明理由．

Answer 1

分析 （1）根据配方法，可得函数的对称轴；
（2）根据自变量与函数值的对应关系，可得A、C点坐标，根据对称性，可得B点坐标，根据待定系数法，可得函数解析式；
（3）根据等腰三角形的定义，可得关于b的方程，根据解方程，可得答案．

解答 解：（1）y=ax²-4ax+2=a（x-2）²+2-4a，
抛物线的对称轴为直线x=2；
（2）当x=0时，y=2，即C点坐标为（0，2），
由OA=OC=2，得A（-2，0），
将A、C点坐标代入函数解析式，得
4a+8a+2=0，解得a=-$\frac{1}{6}$，
抛物线的解析式为y=-$\frac{1}{6}$x²+$\frac{2}{3}$x+2，
由B、C关于对称轴x=2对称，得
B点的纵坐标是2，横坐标是4，即B点的坐标为（4，2）；
（3）存在，设P点坐标为（2，b），
AP²=（2+2）²+b²，PB²=（2-4）²+（b-2）²，AB²=（4+2）²+2²，
当AP=PB时，16+b²=4+（b-2）²，解得b=-2，即P（2，-2）；
当AP=AB时，16+b²=（4+2）²+2²，解得b=2$\sqrt{6}$（不符合题意，舍）b=-2$\sqrt{6}$，即P（2，-2$\sqrt{6}$），
当PB=AB时，（2-4）²+（b-2）²=（4+2）²+2²，解得b=8（不符合题意，舍）b=-4，即P（2，-4），
综上所述：P（2，-2$\sqrt{6}$）（2，-4）（2，-2）．

点评 本题考查了二次函数综合题，利用待定系数法求函数解析式，利用配方法求函数的对称轴是解题关键；利用等腰三角形的定义得出关于b的方程是解题关键．