题目内容
9.已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,A(1,0).(1)若a=-1,函数图象与x轴只有一个交点,求b的值;
(2)若c=1,0<a<1,设B点的横坐标为xB,求证:xB>1;
(3)若a=1,c≥3,问是否存在实数m,使得z=y-m2x在x>0时,z随x的增大而增大?若存在,求m的值;若不存在,请说明理由.
分析 (1)根据条件抛物线化为:y=-x2+bx-b+1,由△=0即可解决问题.
(2)根据条件抛物线化为:y=ax2-(a+1)x+1,令y=0求出点B横坐标即可.
(3)不存在.由题意:z=y-m2x=x2-(c+1+m2)x+c,根据对称轴的位置即可判断.
解答 解:(1)把点A(1,0)代入y=ax2+bx+c得a+b+c=0,
∵a=-1,∴c=-b+1,
∴抛物线为y=-x2+bx-b+1,
由题意△=0,
∴b2-4b+4=0,
∴(b-2)2=0,
∴b=2.
(2)∵b=-a-c,c=1,
∴抛物线为y=ax2-(a+1)x+1,
令y=0,则有ax2-(a+1)x+1=0,
∴(x-1)(ax-1)=0,
∴x=1或$\frac{1}{a}$,
∵0<a<1,
∴$\frac{1}{a}$>1,
∴B点的横坐标为xB>1.
(3)不存在.理由如下:
∵b=-a-c,a=1,
∴b=-1-c,
∴抛物线为y=x2-(c+1)x+c,
∴z=y-m2x=x2-(c+1+m2)x+c,
∵对称轴x=$\frac{c+1+{m}^{2}}{2}$,
又∵c≥3,m2≥0,
∴对称轴x>0.
∴当0<x<$\frac{c+1+{m}^{2}}{2}$时,z随x的增大而减小,
∴这样的m不存在.
点评 本题考查抛物线与x轴交点问题,学会利用参数解决问题是解题的关键,学会分类讨论的思想,属于中考常考题型.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
20. 将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
 将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )| A. | 105° | B. | 115° | C. | 95° | D. | 110° |
13.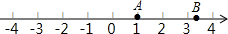 如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )
如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )
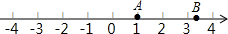 如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )
如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )| A. | -$\sqrt{10}$ | B. | -1-$\sqrt{10}$ | C. | $\sqrt{10}$-2 | D. | 2-$\sqrt{10}$ |
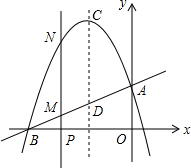 如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为x=-3.
如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为x=-3.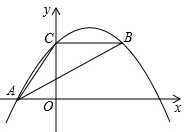 如图,抛物线y=ax2-4ax+2经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且OA=OC.
如图,抛物线y=ax2-4ax+2经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且OA=OC.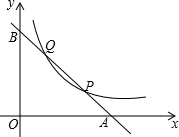 如图,直线y=-x+3与x,y轴分别交于点A,B.与反比例函数y=$\frac{k}{x}$的图象交于点P和点Q,若PQ=2$\sqrt{2}$,则k=$\frac{5}{4}$.
如图,直线y=-x+3与x,y轴分别交于点A,B.与反比例函数y=$\frac{k}{x}$的图象交于点P和点Q,若PQ=2$\sqrt{2}$,则k=$\frac{5}{4}$.