题目内容
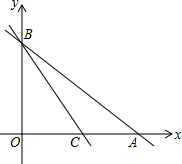 已知直线y=-x+3与x轴、y轴分别交于点A、B,另一直线y=kx+b(k≠0),经过点C(1,0),且把△ABC分成两部分,若△ABC被分成的两部分面积比为1:2,求k和b的值.
已知直线y=-x+3与x轴、y轴分别交于点A、B,另一直线y=kx+b(k≠0),经过点C(1,0),且把△ABC分成两部分,若△ABC被分成的两部分面积比为1:2,求k和b的值.考点:两条直线相交或平行问题
专题:
分析:令y=0,解方程求出OA,令x=0,求出OB,再根据等高的三角形的面积的比等于底边的比分两种情况求出OC,从而得到点C的坐标,再利用待定系数法求一次函数解析式解答.
解答:解:令y=0,则-x+3=0,
解得x=3,
所以,OA=3,
令x=0,则y=3,
所以,OB=3,
所以,点B的坐标为(0,3),
∵△ABC被分成的两部分面积比为1:2,
∴OC=1或OC=2,
当OC=1时,点C的坐标为(1,0),
将B、C的坐标代入y=kx+b得,
,
解得
.
所以y=-3x+3;
当OC=2时,点C的坐标为(2,0),
将B、C的坐标代入y=kx+b得,
,
解得
.
所以y=-
x+3,
综上所述,k和b的值分别为-3和3或-
,3.
解得x=3,
所以,OA=3,
令x=0,则y=3,
所以,OB=3,
所以,点B的坐标为(0,3),
∵△ABC被分成的两部分面积比为1:2,
∴OC=1或OC=2,
当OC=1时,点C的坐标为(1,0),
将B、C的坐标代入y=kx+b得,
|
解得
|
所以y=-3x+3;
当OC=2时,点C的坐标为(2,0),
将B、C的坐标代入y=kx+b得,
|
解得
|
所以y=-
| 3 |
| 2 |
综上所述,k和b的值分别为-3和3或-
| 3 |
| 2 |
点评:本题考查两直线相交的问题,待定系数法求一次函数解析式,等高的三角形的面积的比等于底边的比的性质,难点在于分情况求出点C的坐标.

练习册系列答案
相关题目
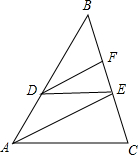 如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,
如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,