题目内容
在一条笔直的公路边,有一些树和路灯,每相邻的两盏灯之间有3棵树,相邻的树与树,树与灯间的距离是10m,如图,第一棵树左边5m处有一个路牌,则从此路牌起向右2015m~2055m之间树与灯的排列顺序是( )


A、 |
B、 |
C、 |
D、 |
考点:规律型:图形的变化类
专题:
分析:根据题意可得,第一个灯的里程数为15m,第二个灯的里程数为55m,第三个灯的里程数为95m…第n个灯的里程数为15+40(n-1)=(40n-25)m,从而可计算出2055m处哪个里程数是灯,也就得出了答案.
解答:解:根据题意得:第一个灯的里程数为15m,
第二个灯的里程数为55m,
第三个灯的里程数为95m
…
第n个灯的里程数为15+40(n-1)=(40n-25)m,
故当n=52时候,40n-25=2055m处是灯,
则2025m、2035m、2045m处均是树,
故应该是树、树、树、灯,
故选C.
第二个灯的里程数为55m,
第三个灯的里程数为95m
…
第n个灯的里程数为15+40(n-1)=(40n-25)m,
故当n=52时候,40n-25=2055m处是灯,
则2025m、2035m、2045m处均是树,
故应该是树、树、树、灯,
故选C.
点评:本题考查了图形的变化类问题,解决本题的关键是从原图中找到规律,并利用规律解决问题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
下列四个数中最小的是( )
| A、0 | ||
| B、0.5 | ||
| C、-1 | ||
D、
|
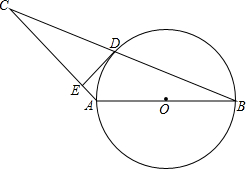 如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于D.过D作DE⊥AC于E.
如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于D.过D作DE⊥AC于E.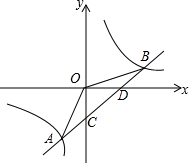 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2=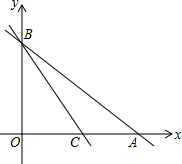 已知直线y=-x+3与x轴、y轴分别交于点A、B,另一直线y=kx+b(k≠0),经过点C(1,0),且把△ABC分成两部分,若△ABC被分成的两部分面积比为1:2,求k和b的值.
已知直线y=-x+3与x轴、y轴分别交于点A、B,另一直线y=kx+b(k≠0),经过点C(1,0),且把△ABC分成两部分,若△ABC被分成的两部分面积比为1:2,求k和b的值. 如图,已知在边长为a的正方形中,剪下一个扇形和一个圆,以此扇形为侧面,圆为底面围成一个圆锥,求此圆锥的表面积.
如图,已知在边长为a的正方形中,剪下一个扇形和一个圆,以此扇形为侧面,圆为底面围成一个圆锥,求此圆锥的表面积.