题目内容
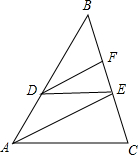如图，在△ABC中，D、E、F分别是AB、BC上的点，且DE∥AC，AE∥DF，| BD |
| AD |
| 3 |
| 2 |
考点：平行线分线段成比例
专题：计算题
分析：根据平行线分线段成比例定理，由AE∥DF得
=
，可计算出EF=4，则BE=BF+EF=10，然后再由DE∥AC得到
=
，可计算出CE=
，所以CF=CE+EF=
．
| BD |
| AD |
| BF |
| EF |
| BD |
| AD |
| BE |
| CE |
| 20 |
| 3 |
| 32 |
| 3 |
解答：解：∵AE∥DF，
∴
=
，即
=
，
∴EF=4，
∴BE=BF+EF=6+4=10，
∵DE∥AC，
∴
=
，即
=
，
∴CE=
，
∴CF=CE+EF=
．
∴
| BD |
| AD |
| BF |
| EF |
| 6 |
| EF |
| 3 |
| 2 |
∴EF=4，
∴BE=BF+EF=6+4=10，
∵DE∥AC，
∴
| BD |
| AD |
| BE |
| CE |
| 10 |
| CE |
| 3 |
| 2 |
∴CE=
| 20 |
| 3 |
∴CF=CE+EF=
| 32 |
| 3 |
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
相关题目
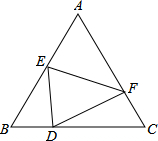如图，已知等边△ABC，现将△ABC折叠，使A点落在BC边上D点，折痕为EF，求证：∠BED=∠FDC．
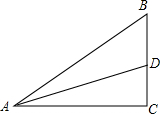在Rt△ABC中，AD是角平分线，已知，AB=5，AC=4，BC=3，∠ACB=90°．
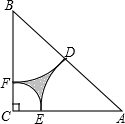如图，在Rt△ABC中，∠C=90°，BC=AC=2cm，分别以A，C，B为圆心作弧，使
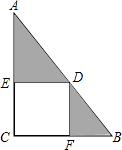如图所示，在Rt△ABC中，∠C=90°，四边形ECFD为正方形，若AD=36，DB=4，求阴影部分的面积．
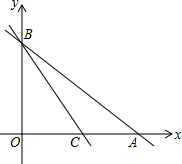已知直线y=-x+3与x轴、y轴分别交于点A、B，另一直线y=kx+b（k≠0），经过点C（1，0），且把△ABC分成两部分，若△ABC被分成的两部分面积比为1：2，求k和b的值．