题目内容
已知方程x2+2（k-4）x+k2+6k+2=0有两个相等的实数根，求k的值，并求出此时方程的根．
考点：根的判别式
专题：
分析：先利用根的判别式求出k的值，再代入方程求根即可．
解答：解：∵方程x2+2（k-4）x+k2+6k+2=0有两个相等的实数根，
∴[2（k-4）]2-4（k2+6k+2）=0，解得k=1，代入方程得x2-6x+9=0，解得x=3．
∴[2（k-4）]2-4（k2+6k+2）=0，解得k=1，代入方程得x2-6x+9=0，解得x=3．
点评：本题主要考查了根的判别式，解题的关键是利用根的判别式求出k的值．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
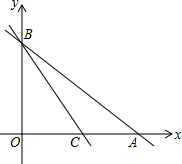已知直线y=-x+3与x轴、y轴分别交于点A、B，另一直线y=kx+b（k≠0），经过点C（1，0），且把△ABC分成两部分，若△ABC被分成的两部分面积比为1：2，求k和b的值．
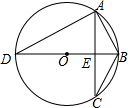已知△ABC中，a、b、c分别为∠A、∠B、∠C的对边，方程ax2+bx-c=0是关于x的一元二次方程．
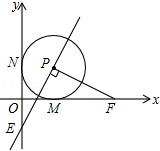已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴，y轴分别相切于点M和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）