题目内容
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上从点A运动到点B,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F
(1)求证:CE=CF;
(2)求线段EF的最小值;
(3)当点D从点A运动到点B时,试求线段EF扫过的面积(直接写出结果).
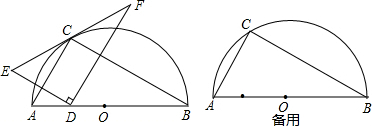
(1)求证:CE=CF;
(2)求线段EF的最小值;
(3)当点D从点A运动到点B时,试求线段EF扫过的面积(直接写出结果).

考点:圆的综合题
专题:
分析:(1)设ED交AC于点G,则点G为ED中点,可证得AC∥DF,得出C为EF中点;
(2)由(1)可知EF=2CD,当CD⊥AB是有最小值,可求得EF的最小值;
(3)当点D从点A运动到点B时,线段EF扫过的面积是△ABC面积的2倍,可求出结果.
(2)由(1)可知EF=2CD,当CD⊥AB是有最小值,可求得EF的最小值;
(3)当点D从点A运动到点B时,线段EF扫过的面积是△ABC面积的2倍,可求出结果.
解答:(1)证明:如图1,设AC于点DE交于点G,则EG=DG,且ED⊥AC,
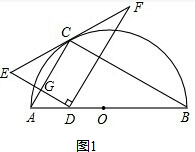
∵DF⊥DE,
∴∠EGC=∠EDF=90°,
∴AC∥DF,且G为ED中点,
∴EC=FC;
(2)解:由(1)知,EF=2CD,
∴当线段EF最小时,线段CD也最小,
根据垂直线段最短的性质,当CD⊥AD时线段CD最小,
∵AB是半圆O 的直径,
∴∠ACB=90°,
∵AB=8,∠CBA=30°,
∴AC=4,BC=4
,
当CD⊥AD时,CD=
BC=2
,
此时EF=2CD=4
,
即EF的最小值为4
;
(3)解:当点D从点A运动到点B时,如图2,EF扫过的图形就是图中的阴影部分,线段EF扫过的面积是△ABC面积的2倍,
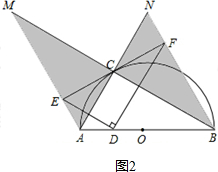
由(2)知AC=4,BC=4
,
∴S△ABC=
•AC•BC=
×4×4
=8
,
∴线段EF扫过的面积是16
.

∵DF⊥DE,
∴∠EGC=∠EDF=90°,
∴AC∥DF,且G为ED中点,
∴EC=FC;
(2)解:由(1)知,EF=2CD,
∴当线段EF最小时,线段CD也最小,
根据垂直线段最短的性质,当CD⊥AD时线段CD最小,
∵AB是半圆O 的直径,
∴∠ACB=90°,
∵AB=8,∠CBA=30°,
∴AC=4,BC=4
| 3 |
当CD⊥AD时,CD=
| 1 |
| 2 |
| 3 |
此时EF=2CD=4
| 3 |
即EF的最小值为4
| 3 |
(3)解:当点D从点A运动到点B时,如图2,EF扫过的图形就是图中的阴影部分,线段EF扫过的面积是△ABC面积的2倍,

由(2)知AC=4,BC=4
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴线段EF扫过的面积是16
| 3 |
点评:本题主要考查圆周角定理及轴对称的性质、勾股定理等知识的综合应用,在第(2)中把EF的值转化成CD的值、在第(3)中确定出EF扫过的面积与△ABC的关系是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
下列四个数中最小的是( )
| A、0 | ||
| B、0.5 | ||
| C、-1 | ||
D、
|
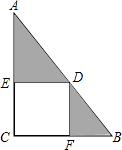 如图所示,在Rt△ABC中,∠C=90°,四边形ECFD为正方形,若AD=36,DB=4,求阴影部分的面积.
如图所示,在Rt△ABC中,∠C=90°,四边形ECFD为正方形,若AD=36,DB=4,求阴影部分的面积.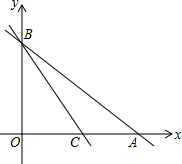 已知直线y=-x+3与x轴、y轴分别交于点A、B,另一直线y=kx+b(k≠0),经过点C(1,0),且把△ABC分成两部分,若△ABC被分成的两部分面积比为1:2,求k和b的值.
已知直线y=-x+3与x轴、y轴分别交于点A、B,另一直线y=kx+b(k≠0),经过点C(1,0),且把△ABC分成两部分,若△ABC被分成的两部分面积比为1:2,求k和b的值. 如图,已知在边长为a的正方形中,剪下一个扇形和一个圆,以此扇形为侧面,圆为底面围成一个圆锥,求此圆锥的表面积.
如图,已知在边长为a的正方形中,剪下一个扇形和一个圆,以此扇形为侧面,圆为底面围成一个圆锥,求此圆锥的表面积.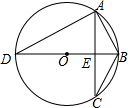 已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程ax2+bx-c=0是关于x的一元二次方程.
已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程ax2+bx-c=0是关于x的一元二次方程.