题目内容
在Rt△ABC中,∠C=90°,根据下列条件解这个直角三角形
(1)c=8
,∠A=60°;
(2)a=6,b=2
.
(1)c=8
| 3 |
(2)a=6,b=2
| 3 |
考点:解直角三角形
专题:
分析:(1)求出∠B,根据含30度角的直角三角形性质求出b,解直角三角形求出a即可;
(2)根据勾股定理求出c,解直角三角形求出∠A,根据三角形内角和定理求出∠B即可.
(2)根据勾股定理求出c,解直角三角形求出∠A,根据三角形内角和定理求出∠B即可.
解答: 解:(1)∵在Rt△ABC中,∠C=90°,∠A=60°,
解:(1)∵在Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=90°-60°=30°,
∵c=8
,
∴b=
c=4
,a=c×sin60°=12.
(2)在Rt△ABC中,∠C=90°,a=6,b=2
,由勾股定理得:c=
=4
,
sinA=
=
=
,
∠A=60°,
所以∠B=90°-∠A=30°.
 解:(1)∵在Rt△ABC中,∠C=90°,∠A=60°,
解:(1)∵在Rt△ABC中,∠C=90°,∠A=60°,∴∠B=90°-60°=30°,
∵c=8
| 3 |
∴b=
| 1 |
| 2 |
| 3 |
(2)在Rt△ABC中,∠C=90°,a=6,b=2
| 3 |
| a2+b2 |
| 3 |
sinA=
| a |
| c |
| 6 | ||
4
|
| ||
| 2 |
∠A=60°,
所以∠B=90°-∠A=30°.
点评:本题考查了含30度角的直角三角形性质,解直角三角形,勾股定理的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
相关题目
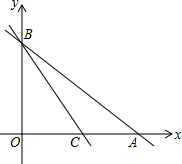 已知直线y=-x+3与x轴、y轴分别交于点A、B,另一直线y=kx+b(k≠0),经过点C(1,0),且把△ABC分成两部分,若△ABC被分成的两部分面积比为1:2,求k和b的值.
已知直线y=-x+3与x轴、y轴分别交于点A、B,另一直线y=kx+b(k≠0),经过点C(1,0),且把△ABC分成两部分,若△ABC被分成的两部分面积比为1:2,求k和b的值.