题目内容
8．
已知如图，在△ABC中，D为AB边上一点，E为AC边上一点，△ADE∽△ACB，AD=4，若AB=6，AE=3，求EC的长．
分析 先根据相似三角形的对应边成比例求出AC的长，再由EC=AC-AE即可得出结论．
解答 解：∵△ADE∽△ACB，AD=4，AB=6，AE=3，
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$，即$\frac{4}{AC}$=$\frac{3}{6}$，解得AC=8，
∴EC=AC-AE=8-3=5．
点评 本题考查的是相似三角形的性质，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．已知反比例函数的图象经过点（2，3），则它的图象一定也经过（ ）
| A． | （-2，-3） | B． | （2，-3） | C． | （-2，3） | D． | （0，0） |
如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要（ ）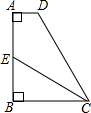
如图，在四边形ABCD中，AD∥BC，AB⊥AD，CE平分∠DCB交AB于E，点E是AB的中点．
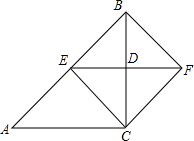如图，在△ABC中，∠A=45°，∠ACB=90°，BC的垂直平分线EF交BC于D，交AB于E，且CF=BE．求证：四边形BECF是正方形．