题目内容
16.△ABC中,若∠A=2∠B=3∠C,AC=2$\sqrt{3}$cm,则∠A=90度,∠B=60度,∠C=30度,BC=4cm,S△ABC=2$\sqrt{3}$cm2.分析 根据三角形内角和定理和已知条件易求得△ABC的三个内角的度数,然后由勾股定理可以求得AB、BC的长度.最后根据三角形的面积公式求得其面积.
解答  解:∵在△ABC中,∠A=2∠B=3∠C,∠A+∠B+∠C=180°,
解:∵在△ABC中,∠A=2∠B=3∠C,∠A+∠B+∠C=180°,
∴∠A=90°,∠B=60°,∠C=30°.
∴AB=$\frac{1}{2}$BC,BC2=AC2+AB2,
又∵AC=2$\sqrt{3}$cm,
∴BC=4cm,AB=2cm,
∴S△ABC=$\frac{1}{2}$AC•AB=$\frac{1}{2}$×2$\sqrt{3}$2=2$\sqrt{3}$(cm2).
故答案是:90;60;30;4cm;2$\sqrt{3}$cm2.
点评 本题考查了勾股定理,含30度的直角三角形.该性质是直角三角形中含有特殊度数的角(30°)的特殊定理,非直角三角形或一般直角三角形不能应用.

练习册系列答案
相关题目
11.在下列四组线段中,能组成直角三角形的是( )
| A. | a=32,b=42,c=52 | B. | a=11,b=12,c=13 | C. | a=9,b=40,c=41 | D. | a:b:c=1:1:2 |
 通过计算几何图形的面积可表示一些代数恒等式(一定成立的等式),请根据图写出一个代数恒等式是:2a(a+b)=2a2+2ab.
通过计算几何图形的面积可表示一些代数恒等式(一定成立的等式),请根据图写出一个代数恒等式是:2a(a+b)=2a2+2ab.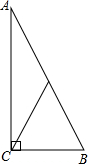 已知:在Rt△ABC中.∠ACB=90°,斜边的中线长3,sinA=$\frac{1}{3}$.求△ABC的面积.
已知:在Rt△ABC中.∠ACB=90°,斜边的中线长3,sinA=$\frac{1}{3}$.求△ABC的面积. 已知如图,在△ABC中,D为AB边上一点,E为AC边上一点,△ADE∽△ACB,AD=4,若AB=6,AE=3,求EC的长.
已知如图,在△ABC中,D为AB边上一点,E为AC边上一点,△ADE∽△ACB,AD=4,若AB=6,AE=3,求EC的长. 正方形ABCD的边长为3,它的四个顶点在直角坐标系中的位置如图所示,求它四个顶点的坐标.
正方形ABCD的边长为3,它的四个顶点在直角坐标系中的位置如图所示,求它四个顶点的坐标.