题目内容
13.已知两个多边形的内角和为1800°,且这两个多边形的边数均为偶数,求这两个多边形的边数.分析 设两个多边形的边数分别为m、n,然后根据多边形的内角和公式求得m+n的值,然后可求得这两个多边形的边数.
解答 解:设这两个多边形的边数分别为m、n.
根据题意得:(m-2)×180°+(n-2)×180°=1800°.
∴m+n=14.
∵m、n均为偶数,且m、n都大于2,
∴m、n的值为4和10或6和8.
∴这两个多边形的边数为4和10或6和8.
点评 本题主要考查的是多边形的内角和公式的应用,根据多边形的内角和公式求得n+m=14是解题的关键.

练习册系列答案
相关题目
18.某书店为提倡人们“多读书,读好书”,每年都要开展“过三关”免费赠书活动,今年赠书活动的前提是:顺利通过书店设置的三关,在每关内放置一道题.若能在规定的时间内顺利答对这三道题,就可免费得到赠书,同学们你们想参加吗?快快行动吧!
| 第一关 | 第二关 | 第三关 |
| 若x=-1是关于x的一元二次方程ax2+bx+c=0(b≠0)的一个根,则$\frac{a}{b}+\frac{c}{b}$= 1 | 若3a+6>0,且ax2-5x+3=0是关于x的一元二次方程,则a的取值范围是 a>-2且a≠0 | 若代数式2x2+3x+7的值是8,则代数式4x2+6x-9的值为 -7 |
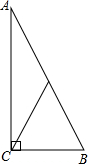 已知:在Rt△ABC中.∠ACB=90°,斜边的中线长3,sinA=$\frac{1}{3}$.求△ABC的面积.
已知:在Rt△ABC中.∠ACB=90°,斜边的中线长3,sinA=$\frac{1}{3}$.求△ABC的面积. 已知如图,在△ABC中,D为AB边上一点,E为AC边上一点,△ADE∽△ACB,AD=4,若AB=6,AE=3,求EC的长.
已知如图,在△ABC中,D为AB边上一点,E为AC边上一点,△ADE∽△ACB,AD=4,若AB=6,AE=3,求EC的长. 正方形ABCD的边长为3,它的四个顶点在直角坐标系中的位置如图所示,求它四个顶点的坐标.
正方形ABCD的边长为3,它的四个顶点在直角坐标系中的位置如图所示,求它四个顶点的坐标.
 如图所示,以∠B为内角的三角形共有3个.
如图所示,以∠B为内角的三角形共有3个.