Question

18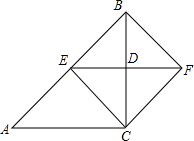．如图，在△ABC中，∠A=45°，∠ACB=90°，BC的垂直平分线EF交BC于D，交AB于E，且CF=BE．求证：四边形BECF是正方形．

Answer 1

分析 先根据中垂线的性质得出BE=EC，BF=FC，由CF=BE，等量代换得出BE=EC=BF=FC，那么四边形BECF是菱形；再由∠A=45°，∠ACB=90°，根据三角形内角和定理及等腰三角形的性质求出∠BEC=90°，于是菱形BECF是正方形．

解答 证明：∵EF垂直平分BC，
∴BE=EC，BF=CF，
∵CF=BE，
∴BE=EC=CF=BF，
∴四边形BECF是菱形；
∵∠A=45°，∠ACB=90°，
∴∠EBC=45°，
∵BE=EC，
∴∠ECB=∠EBC=45°，
∴∠BEC=90°，
∴菱形BECF是正方形．

点评 本题考查了正方形的判定方法：
①先判定四边形是矩形，再判定这个矩形有一组邻边相等；
②先判定四边形是菱形，再判定这个菱形有一个角为直角；
③还可以先判定四边形是平行四边形，再用1或2进行判定．
同时考查了线段垂直平分线的性质，三角形内角和定理及等腰三角形的性质．