题目内容
4.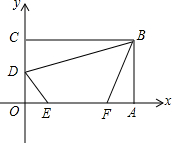 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )| A. | ($\frac{1}{2}$,0) | B. | ($\frac{4}{3}$,0) | C. | ($\frac{3}{2}$,0) | D. | (2,0) |
分析 将点B向左平移2个单位得到B′(4,4),作点D关于x轴的对称点D′(0,-2),连接B′D′与x轴的交点为E,此时四边形BDEF周长最小,求出直线B′D′的解析式即可解决问题.
解答 解:如图,将点B向左平移2个单位得到B′(4,4),作点D关于x轴的对称点D′(0,-2),连接B′D′与x轴的交点为E,此时四边形BDEF周长最小,
理由∵四边形BDEF的周长为BD+DE+EF+BF,BD与EF是定值,
∴BF+DE最小时,四边形BDEF周长最小,
∵BF+ED=B′E+ED′=B′D′
设直线B′D′为y=kx+b,把(4,4),(0,-2)代入得$\left\{\begin{array}{l}{4k+b=4}\\{b=-2}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-2}\end{array}\right.$,
∴直线B′D′为y=$\frac{3}{2}$x-2,
令y=0,得x=$\frac{4}{3}$,
∴点E坐标($\frac{4}{3}$,0).
故选B.
点评 本题考查轴对称-最短问题、坐标与图形性质、一次函数等知识,解题的关键是正确找到点E、F的位置,利用一次函数解决交点坐标问题,是数形结合的好题目,属于中考常考题型.

练习册系列答案
相关题目
12.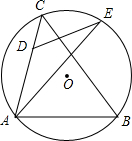 如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
 如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
16.若x,y都是有理数,且|4-3x+y|与(3-4x-y)2互为相反数,则x,y的值分别为( )
| A. | x=-1,y=2 | B. | x=1,y=-1 | C. | x=0,y=-$\frac{3}{5}$ | D. | x=3,y=1 |
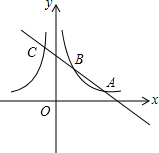 函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)的图象关于y轴对称,我们定义函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)相互为“影像”函数
函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)的图象关于y轴对称,我们定义函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)相互为“影像”函数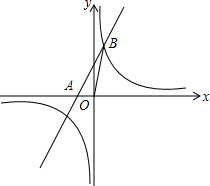 如图,直线y=2x+3与反比例函数y=$\frac{k}{x}$的图象相交于点B(a,5),且与x轴相交于点A.
如图,直线y=2x+3与反比例函数y=$\frac{k}{x}$的图象相交于点B(a,5),且与x轴相交于点A.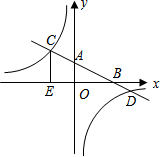 如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.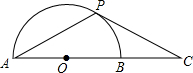 如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA
如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA