题目内容
13.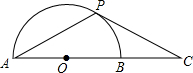 如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA
如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA(1)如果BC=OA,求证:PC是⊙O的切线;
(2)设AB=8,AP=x,当直线PC与⊙O相交时,求x的取值范围.
分析 (1)只需证明OP⊥CP即可;
(2)分两种情况:①当PC和PB重合时,证得△ACP是等腰直角三角形,即可求得AP=4$\sqrt{2}$,②当PC与⊙O相切时,证得△OPB是等边三角形,即可求得AP=4$\sqrt{3}$,从而求得x的取值范围.
解答 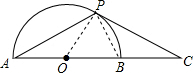 (1)证明:连接OP,BP,
(1)证明:连接OP,BP,
∵AB是直径,
∴∠APB=90°,
∵PA=PC,
∴∠A=∠C,
∵BC=OA,
∴AB=OC,
在△APB和△CPO中,
$\left\{\begin{array}{l}{PA=PC}\\{∠A=∠C}\\{AB=OC}\end{array}\right.$,
∴△APB≌△CPO(SAS),
∴∠OPC=∠APB=90°,
即OP⊥PC,
∴PC是⊙O的切线.
(2)当PC和PB重合时,
∵PC=PA,
∴△ACP是等腰直角三角形,
∵AC=AB=8,
∴AP=4$\sqrt{2}$,
当PC与⊙O相切时,∵AB是直径,
∴∠APB=90°,
∵PA=PC,
∴∠A=∠C,
在△APB和△CPO中,
$\left\{\begin{array}{l}{∠A=∠C}\\{PA=PC}\\{∠APB=∠CPO=90°}\end{array}\right.$,
∴△APB≌△CPO(ASA),
∴OP=BP,
∴OP=BP=OB,
∴△OPB是等边三角形,
∴∠ABP=60°,
∴PA=$\frac{\sqrt{3}}{2}$AB=4$\sqrt{3}$,
∴当直线PC与⊙O相交时,求x的取值范围上4$\sqrt{2}$<x<4$\sqrt{3}$.
点评 本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
4.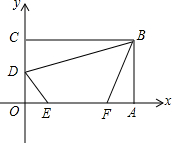 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )| A. | ($\frac{1}{2}$,0) | B. | ($\frac{4}{3}$,0) | C. | ($\frac{3}{2}$,0) | D. | (2,0) |
5.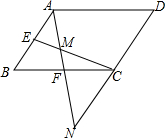 如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
(1)求证:AB=CN;
(2)若△AEM的面积为2,求?ABCD的面积.
 如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.(1)求证:AB=CN;
(2)若△AEM的面积为2,求?ABCD的面积.
2.若m<0,则不等式组$\left\{\begin{array}{l}{x<-\frac{m}{3}}\\{x<-\frac{m}{4}}\end{array}\right.$的解集是( )
| A. | x<$\frac{m}{3}$ | B. | x<-$\frac{m}{4}$ | C. | x<-$\frac{m}{3}$ | D. | x<$\frac{m}{4}$ |
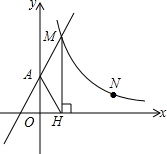 如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2. 已知A(2,-2),B(-1,4)是一次函数y2=-2x+2的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.
已知A(2,-2),B(-1,4)是一次函数y2=-2x+2的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.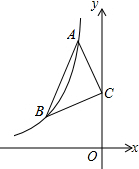 如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.