题目内容
10.k是正整数,ak,bk是关于x的方程x2-[(k+1)$\sqrt{k}$+k$\sqrt{k+1}$]x-1=0的两个根,那么$\frac{1}{{a}_{1}+{b}_{1}}$+$\frac{1}{{a}_{2}+{b}_{2}}$+…+$\frac{1}{{a}_{2011}+{b}_{2011}}$=$\frac{1006-\sqrt{503}}{1006}$.分析 由根与系数的关系可得出ak+bk的值,取其倒数进行化简后得$\frac{1}{{a}_{k}+{b}_{k}}$=$\frac{1}{\sqrt{k}}$-$\frac{1}{\sqrt{k+1}}$,将其代入所给算式中即可得出结论.
解答 解:∵ak,bk是关于x的方程x2-[(k+1)$\sqrt{k}$+k$\sqrt{k+1}$]x-1=0的两个根,
∴ak+bk=(k+1)$\sqrt{k}$+k$\sqrt{k+1}$,$\frac{1}{{a}_{k}+{b}_{k}}$=$\frac{1}{(k+1)\sqrt{k}+k\sqrt{k+1}}$=$\frac{1}{\sqrt{k}}$-$\frac{1}{\sqrt{k+1}}$.
∴$\frac{1}{{a}_{1}+{b}_{1}}$+$\frac{1}{{a}_{2}+{b}_{2}}$+…+$\frac{1}{{a}_{2011}+{b}_{2011}}$=$\frac{1}{1}$-$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{2}}$-$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{2011}}$-$\frac{1}{\sqrt{2012}}$=1-$\frac{1}{\sqrt{2012}}$=$\frac{2012-\sqrt{2012}}{2012}$=$\frac{1006-\sqrt{503}}{1006}$.
故答案为:$\frac{1006-\sqrt{503}}{1006}$.
点评 本题考查了根与系数的关系以及分式的化简,解题的关键是找出$\frac{1}{{a}_{k}+{b}_{k}}$=$\frac{1}{\sqrt{k}}$-$\frac{1}{\sqrt{k+1}}$.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系得出两根的和,将其代入所给算式中求和即可.

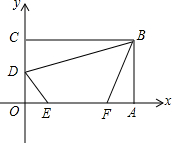 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )| A. | ($\frac{1}{2}$,0) | B. | ($\frac{4}{3}$,0) | C. | ($\frac{3}{2}$,0) | D. | (2,0) |
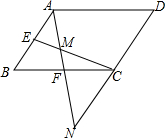 如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.(1)求证:AB=CN;
(2)若△AEM的面积为2,求?ABCD的面积.
| A. | x<$\frac{m}{3}$ | B. | x<-$\frac{m}{4}$ | C. | x<-$\frac{m}{3}$ | D. | x<$\frac{m}{4}$ |
 如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )
如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )| A. | 45° | B. | 60° | C. | 90° | D. | 180° |
 如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.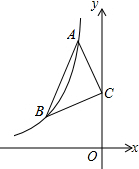 如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.