题目内容
12.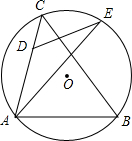 如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 连接CE,根据∠ABC=∠AEC且∠CDE=∠ABC可得∠AEC=∠EDC,可证得△ACE∽△ECD,得出$\frac{AE}{DE}$=$\frac{AC}{CE}$=$\frac{CE}{DC}$,设CD=x,则AD=2x,AC=3x,分别表示出AC的长,进而表示出CE的长,可得AE:DE的值.
解答 解:连接CE,如图所示: ∵∠ABC=∠AEC,∠CDE=∠ABC,
∵∠ABC=∠AEC,∠CDE=∠ABC,
∴∠AEC=∠EDC,
又∵∠ACE=∠ECD,
∴△ACE∽△ECD,
∴$\frac{AE}{DE}$=$\frac{AC}{CE}$=$\frac{CE}{DC}$,∵AD=2CD,
∴$\frac{AD}{CD}$=2,
设CD=x,则AD=2x,AC=3x,
则CE2=AC•DC=3x2,
得:CE=$\sqrt{3}$x
∴$\frac{AE}{DE}$=$\frac{AC}{CE}$=$\frac{3x}{\sqrt{3}x}$=$\sqrt{3}$;
故选:C.
点评 本题主要考查相似三角形的性质与判定及圆周角定理的运用,根据圆周角定理得出两角相等是证明三角形相似的前提,根据相似性质得到对应边成比例是关键.

练习册系列答案
相关题目
2.若x与2互为相反数,则|x+2|的值是( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
17.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③x=2是方程ax2+(b-1)x+c=0的一个根;
④当-1<x<2时,ax2+(b-1)x+c>0.
上述结论中正确的有( )个.
| x | -1 | 0 | 0.5 | 2 |
| y | -1 | 2 | 3.75 | 2 |
②当x>1时,y的值随x值的增大而减小;
③x=2是方程ax2+(b-1)x+c=0的一个根;
④当-1<x<2时,ax2+(b-1)x+c>0.
上述结论中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.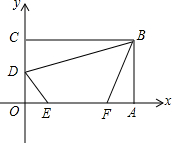 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )| A. | ($\frac{1}{2}$,0) | B. | ($\frac{4}{3}$,0) | C. | ($\frac{3}{2}$,0) | D. | (2,0) |
2.若m<0,则不等式组$\left\{\begin{array}{l}{x<-\frac{m}{3}}\\{x<-\frac{m}{4}}\end{array}\right.$的解集是( )
| A. | x<$\frac{m}{3}$ | B. | x<-$\frac{m}{4}$ | C. | x<-$\frac{m}{3}$ | D. | x<$\frac{m}{4}$ |
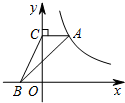 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AC⊥y轴于点C,点B在x轴上,连结CB、AB.若△ABC的面积为4,则k的值为8.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AC⊥y轴于点C,点B在x轴上,连结CB、AB.若△ABC的面积为4,则k的值为8.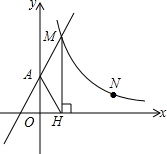 如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.