题目内容
17.已知a2+b2-4a+2b+5=0,先化简,再求值:$\frac{1}{2}$[($\frac{a}{2}$+b)2+($\frac{a}{2}$-b)2](a2-4b2).分析 首先配方,根据非负数的性质求出a和b的值,然后去括号化简,最后代值计算.
解答 解:∵a2+b2-4a+2b+5=0,
∴a2-4a+4+b2+2b+1=0,
∴(a-2)2+(b+1)2=0,
∴a-2=0且b+1=0,
∴a=2,b=-1,
∴$\frac{a}{2}$-b=2,$\frac{a}{2}$+b=0,
原式=$\frac{1}{2}$[($\frac{a}{2}$+b)2+($\frac{a}{2}$-b)2](a-2b)(a+2b)
=$\frac{1}{2}$[($\frac{a}{2}$+b)2+($\frac{a}{2}$-b)2]×2($\frac{a}{2}$-b)×2($\frac{a}{2}$+b)
=2[($\frac{a}{2}$+b)2+($\frac{a}{2}$-b)2]($\frac{a}{2}$-b)($\frac{a}{2}$+b)
所以把$\frac{a}{2}$-b=2,$\frac{a}{2}$+b=0代入化简的式子中得到原式=2(0+22)×0×2=0.
点评 本题主要考查了整式的混合运算-化简求值的知识,解答本题的关键是熟练掌握完全平方公式以及多项式乘法的运算法则以及能根据非负数的性质求出a和b的值,此题难度不大.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
9.一个四边形四个外角之比为1:2:3;4,则这个四边形的内角中( )
| A. | 只有一个锐角 | B. | 有两个锐角 | C. | 有三个锐角 | D. | 有四个锐角 |
12.将二次函数y=x2+1的图象向上平移2个单位,再向右平移1个单位,平移后的函数解析式为( )
| A. | y=(x-1)2-1 | B. | y=(x+1)2-1 | C. | y=(x+1)2+3 | D. | y=(x-1)2+3 |
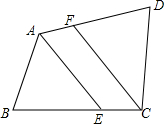 如图,已知四边形ABCD中,∠B=∠D,AE平分∠DAB,AE∥FC,求证:CF平分∠BCD.
如图,已知四边形ABCD中,∠B=∠D,AE平分∠DAB,AE∥FC,求证:CF平分∠BCD.