题目内容
8.利用判别式判断下列方程的根的情况:(1)2x2-3x-$\frac{3}{2}$=0;
(2)16x2-24x+9=0;
(3)x2-4$\sqrt{2}$x+9=0;
(4)3x2+10=2x2+8x.
分析 (1)直接计算判别式的值,然后根据判别式的意义判断方程根的情况;
(2)直接计算判别式的值,然后根据判别式的意义判断方程根的情况;
(3)直接计算判别式的值,然后根据判别式的意义判断方程根的情况;
(4)先化为一般式,再计算判别式的值,然后根据判别式的意义判断方程根的情况.
解答 解:(1)2x2-3x-$\frac{3}{2}$=0,
∵△=(-3)2-4×2×(-$\frac{3}{2}$)=21>0,
∴方程有两个不相等的实数根;
(2)16x2-24x+9=0,
∵△=(-24)2-4×16×9=0,
∴方程有两个相等的实数根;
(3)x2-4$\sqrt{2}$x+9=0,
∵△=(-4$\sqrt{2}$)2-4×1×9=-4<0,
∴方程无实数根;
(4)3x2+10=2x2+8x,
x2-8x+10=0,
∵△=(-8)2-4×1×10=24>0,
∴方程有两个不相等的实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
13.如下表,方程1、方程2、方程3…是按照一定的规律排列的一列方程,解方程3,并将它的解填在表中的空白处.
(1)请写出这列方程中第m个方程,并写出它的解.
(2)用你探究的规律解方程x2-8x-20=0.
| 序号 | 方程 | 方程的解 | |
| 1 | x2+2x-3=0 | x1=1 | x2=-3 |
| 2 | x2+4x-12=0 | x1=2 | x2=-6 |
| 3 | x2+6x-27=0 | x1=3 | x2=-9 |
| … | … | … | … |
(2)用你探究的规律解方程x2-8x-20=0.
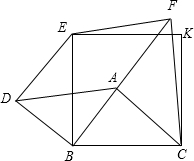 已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.
已知,A是正方形EKCB内的任意点,分别以AB、AC为直角边,按如图方式作等腰直角三角形,即Rt△ABD、Rt△FAC,又∠ABD=∠FAC=90°,连接DE、EF.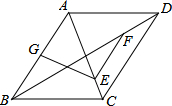 如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.
如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.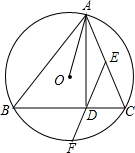 如图,已知△ABC内接于⊙O,AD⊥BC于D,E为AC的中点,延长ED交⊙O于F.
如图,已知△ABC内接于⊙O,AD⊥BC于D,E为AC的中点,延长ED交⊙O于F.