题目内容
5.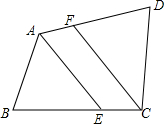 如图,已知四边形ABCD中,∠B=∠D,AE平分∠DAB,AE∥FC,求证:CF平分∠BCD.
如图,已知四边形ABCD中,∠B=∠D,AE平分∠DAB,AE∥FC,求证:CF平分∠BCD.
分析 由平行线的性质可得到∠DFC=∠FAE,结合角平分线的定义和已知条件可求得∠DCF=∠BAE,可求得∠DCF=∠BEA=∠FCB,可证得结论.
解答 证明:∵AE∥CF,
∴∠DFC=∠DAE,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DFC=∠BAE,
又∵∠B=∠D,
∴∠AEB=∠DCF,
又∵AE∥CF,
∴∠BCF=∠BEA,
∴∠DCF=∠BCF,
∴CF平分∠BCD.
点评 本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
13.如下表,方程1、方程2、方程3…是按照一定的规律排列的一列方程,解方程3,并将它的解填在表中的空白处.
(1)请写出这列方程中第m个方程,并写出它的解.
(2)用你探究的规律解方程x2-8x-20=0.
| 序号 | 方程 | 方程的解 | |
| 1 | x2+2x-3=0 | x1=1 | x2=-3 |
| 2 | x2+4x-12=0 | x1=2 | x2=-6 |
| 3 | x2+6x-27=0 | x1=3 | x2=-9 |
| … | … | … | … |
(2)用你探究的规律解方程x2-8x-20=0.
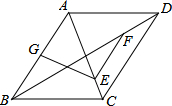 如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.
如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.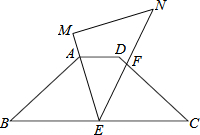 如图,等腰梯形ABCD中,AD∥BC,AD=$\sqrt{2}$,BC=4$\sqrt{2}$,∠B=45°,等腰直角三角板MEN的锐角顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于$\frac{5}{2}$或4$\sqrt{2}$-3或2.
如图,等腰梯形ABCD中,AD∥BC,AD=$\sqrt{2}$,BC=4$\sqrt{2}$,∠B=45°,等腰直角三角板MEN的锐角顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于$\frac{5}{2}$或4$\sqrt{2}$-3或2.