题目内容
9.一个四边形四个外角之比为1:2:3;4,则这个四边形的内角中( )| A. | 只有一个锐角 | B. | 有两个锐角 | C. | 有三个锐角 | D. | 有四个锐角 |
分析 先根据四边形的四个外角的度数之比分别求出四个外角,再根据多边形外角与内角的关系分别求出它们的内角,从而求解.
解答 解:∵一个四边形四个外角的度数之比为1:2:3:4,
∴四个外角的度数分别为:360°×$\frac{1}{1+2+3+4}$=36°;
360°×$\frac{2}{1+2+3+4}$=72°;
360°×$\frac{3}{1+2+3+4}$=108°;
360°×$\frac{4}{1+2+3+4}$=144°.
∴四个内角的度数分别为:180°-36°=144°;
180°-72°=108°;
180°-108°=72°;
180°-144°=36°,
这个四边形的内角中有两个锐角.
故选:B.
点评 此题考查了多边形的外角和的特征:多边形的外角和是固定的360°,结合多边形的内角与外角的关系来求解.

练习册系列答案
相关题目
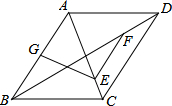 如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.
如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.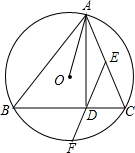 如图,已知△ABC内接于⊙O,AD⊥BC于D,E为AC的中点,延长ED交⊙O于F.
如图,已知△ABC内接于⊙O,AD⊥BC于D,E为AC的中点,延长ED交⊙O于F.