题目内容
求m为何值时，多项式x2-y2+mx+5y-6能因式分解，并分解此多项式．
考点：因式分解-十字相乘法等
专题：计算题
分析：由多项式能分解因式，利用十字相乘法求出m的值，确定出多项式，分解即可．
解答：解：∵x2-y2+mx+5y-6=x2+mx-（y2-5y+6）=x2+mx-（y-3）（y-2），
∴由十字相乘法，得m=-（y-3）+（y+2）=1 或m=（y-3）+[-（y-2）]=-1，
∴m=±1时，多项式x2-y2+mx+5y-6能因式分解，
当m=1时，x2-y2+mx+5y-6=[x-（y-3）][x+（y-2）]=（x-y+3）（x+y-2）；
当m=-1时，x2-y2+mx+5y-6=[x+（y-3）][x-（y-2）]=（x+y-3）（x-y+2）．
∴由十字相乘法，得m=-（y-3）+（y+2）=1 或m=（y-3）+[-（y-2）]=-1，
∴m=±1时，多项式x2-y2+mx+5y-6能因式分解，
当m=1时，x2-y2+mx+5y-6=[x-（y-3）][x+（y-2）]=（x-y+3）（x+y-2）；
当m=-1时，x2-y2+mx+5y-6=[x+（y-3）][x-（y-2）]=（x+y-3）（x-y+2）．
点评：此题考查了因式分解-十字相乘法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
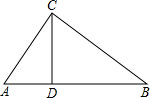如图所示，已知△ABC中，∠C=90°，CD⊥AB，垂足为D，已知AC=3，BC=4． 
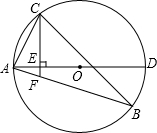如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，作CE⊥AD，垂足为E，CE的延长线与AB交于F．试分析∠ACF与∠ABC是否相等，并说明理由．
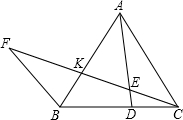如图，在等边△ABC中，K、D两点分别在AB、BC上，BK=CD，连接AD、CK并延长CK至点F，连接FB，∠F=30°．
如图，△ABC中，DE∥AC，DF∥AB，证明：△ABC的内角和为180°．
