题目内容
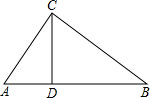 如图所示,已知△ABC中,∠C=90°,CD⊥AB,垂足为D,已知AC=3,BC=4.
如图所示,已知△ABC中,∠C=90°,CD⊥AB,垂足为D,已知AC=3,BC=4. (1)线段AD,CD,CD,BD是不是成比例线段?写出你的理由.
(2)在这个图形中能否再找出其他成比例的四条线段?如果有,请至少写出两组.
考点:相似三角形的判定与性质,比例线段
专题:
分析:(1)运用△ADC∽△CDB,即可得出线段AD,CD,CD,BD成比例线段.
(2)利用直角三角形斜边上的高的性质得出线段成比例.
(2)利用直角三角形斜边上的高的性质得出线段成比例.
解答:解:(1)线段AD,CD,CD,BD成比例线段.
理由:∵∠C=90°,CD⊥AB,
∴∠CDA=∠BDC=90°,∠A=∠BCD,
∴△ADC∽△CDB,
∴AD:CD=CD:BD,
∴线段AD,CD,CD,BD成比例线段.
(2)①AD,AC,AC,AB四条线段成比例,
②BD,BC,BC,AB四条线段成比例.
理由:∵∠C=90°,CD⊥AB,
∴∠CDA=∠BDC=90°,∠A=∠BCD,
∴△ADC∽△CDB,
∴AD:CD=CD:BD,
∴线段AD,CD,CD,BD成比例线段.
(2)①AD,AC,AC,AB四条线段成比例,
②BD,BC,BC,AB四条线段成比例.
点评:本题主要考查了相似三角形的判定与性质及比例线段,解题的关键是利用相似三角形的判定与性质证得线段成比例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果以扇形的半径为直径作一个圆,这个圆的面积恰好与扇形的面积相等,则扇形圆心角的度数为( )
| A、60° | B、90° |
| C、120° | D、150° |
下列语句:
①形状相同的三角形是全等三角形;
②有两边及一角对应相等的两个三角形全等;
③两个等边三角形一定全等;
④有两角一边对应相等的两个三角形全等.
其中错误的说法个数有( )
①形状相同的三角形是全等三角形;
②有两边及一角对应相等的两个三角形全等;
③两个等边三角形一定全等;
④有两角一边对应相等的两个三角形全等.
其中错误的说法个数有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
若a×
=c×
=b×
,且a、b、c都大于0,则它们中最大的是( )
| 2009 |
| 2010 |
| 2010 |
| 2011 |
| 2011 |
| 2012 |
| A、a | B、b | C、c | D、无法确定 |
 如图,AB为⊙O的直径,AB=10cm,动弦CD=6cm,动弦CD始终与AB相交,问当CD弦在⊙O上滑动时,A、B到直线CD距离之差的绝对值是否发生变化?若变化,请说明理由;若不变,予以证明并求其值.
如图,AB为⊙O的直径,AB=10cm,动弦CD=6cm,动弦CD始终与AB相交,问当CD弦在⊙O上滑动时,A、B到直线CD距离之差的绝对值是否发生变化?若变化,请说明理由;若不变,予以证明并求其值.