题目内容
四边形ABCD中,∠B=∠D=90°,∠BAD=60°,且AB=500m,CD=100m,求四边形ABCD的面积.
考点:解直角三角形
专题:
分析:在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后再代入三角函数进行求解,分别延长AD、BC交于点E,根据四边形ABCD的面积=S△ABE-S△CDE求解.
解答: 解:如图,延长AD、BC交于点E.
解:如图,延长AD、BC交于点E.
在Rt△ABE中,∵∠B=90°,∠BAD=60°,AB=500m,
∴∠E=30°,
∴BE=AB•tan60°=500
m,
∴S△ABE=
AB•BE=
×500×500
=125000
(cm2).
在Rt△CDE中,∵∠CDE=90°,∠E=30°,CD=100m,
∴CE=2CD=200m,DE=
CD=100
m,
∴S△CDE=
CD•DE=
×100×100
=5000
(cm2),
∴四边形ABCD的面积=S△ABE-S△CDE=125000
-5000
=120000
(cm2).
 解:如图,延长AD、BC交于点E.
解:如图,延长AD、BC交于点E.在Rt△ABE中,∵∠B=90°,∠BAD=60°,AB=500m,
∴∠E=30°,
∴BE=AB•tan60°=500
| 3 |
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△CDE中,∵∠CDE=90°,∠E=30°,CD=100m,
∴CE=2CD=200m,DE=
| 3 |
| 3 |
∴S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴四边形ABCD的面积=S△ABE-S△CDE=125000
| 3 |
| 3 |
| 3 |
点评:本题考查了解直角三角形,通过作辅助线,构造新的直角三角形,利用四边形ABCD的面积=S△ABE-S△CDE来求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若a×
=c×
=b×
,且a、b、c都大于0,则它们中最大的是( )
| 2009 |
| 2010 |
| 2010 |
| 2011 |
| 2011 |
| 2012 |
| A、a | B、b | C、c | D、无法确定 |
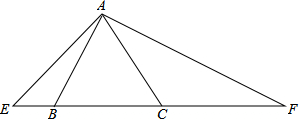 已知∠EAF=120°,它绕着边长为2的正△ABC的顶点A旋转,在正△ABC的左侧,右侧分别交直线BC于E,F.求BE•CF的值.
已知∠EAF=120°,它绕着边长为2的正△ABC的顶点A旋转,在正△ABC的左侧,右侧分别交直线BC于E,F.求BE•CF的值.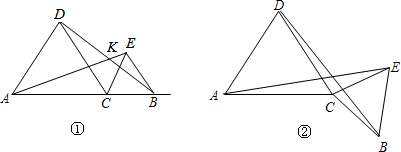
 如图,在⊙O中,BC、CD为⊙O的弦,过O作OA⊥BC交⊙O于点A,连接AD,若∠CDA=25°,∠AOB的度数是多少?
如图,在⊙O中,BC、CD为⊙O的弦,过O作OA⊥BC交⊙O于点A,连接AD,若∠CDA=25°,∠AOB的度数是多少?