题目内容
 如图,已知OA⊥OB,OC⊥OD,O为垂足,若∠AOD=138°,求∠BOC的度数.
如图,已知OA⊥OB,OC⊥OD,O为垂足,若∠AOD=138°,求∠BOC的度数.考点:垂线
专题:
分析:根据垂线的定义,可得∠AOC、∠BOD的度数,根据角的和差,可得∠COD的度数,根据角的和差,可得答案.
解答:解:由OA⊥OB,OC⊥OD,O为垂足,得
∠AOC=∠BOD=90°.
由角的和差,得
∠COD=∠AOD-∠AOC=138°-90°=48°,
∠BOC=∠BOD-∠COD=90°-48°=42°.
∠AOC=∠BOD=90°.
由角的和差,得
∠COD=∠AOD-∠AOC=138°-90°=48°,
∠BOC=∠BOD-∠COD=90°-48°=42°.
点评:本题考查了垂线,利用了垂线的定义,角的和差.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
一个多边形的内角和等于它的外角和的3倍,它是( )
| A、八边形 | B、七边形 |
| C、六边形 | D、五边形 |
 如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠A=70°,则∠F的度数为( )
如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠A=70°,则∠F的度数为( )| A、110° | B、125° |
| C、130° | D、135° |
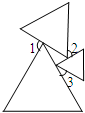 三个等边三角形的位置如图所示,若∠1+∠3=122°,则∠2=
三个等边三角形的位置如图所示,若∠1+∠3=122°,则∠2=