题目内容
PA、PB分别切⊙O于A、B两点,C为⊙O上一动点(点C不与A、B重合),∠APB=50°,则∠ACB为 .
考点:切线的性质
专题:分类讨论
分析:连结OA、OB,如图,先根据切线的性质得∠PAO=∠PBO=90°,再根据四边形内角和计算出∠AOB=180°-∠APB=130°,然后分类讨论:当点C在优弧AB上,根据圆周角定理易得∠ACB=
∠AOB=65°;当点C在劣弧AB上,即C′的位置,根据圆内接四边形的性质易得∠AC′B=180°-∠ACB=115°.
| 1 |
| 2 |
解答:解: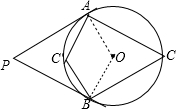 连结OA、OB,如图,
连结OA、OB,如图,
∵PA、PB分别切⊙O于A、B两点,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∴∠AOB=180°-∠APB=180°-50°=130°,
当点C在优弧AB上,则∠ACB=
∠AOB=65°;
当点C在劣弧AB上,即C′的位置,则∠AC′B=180°-∠ACB=180°-65°=115°,
即∠ACB为65°或115°.
故答案为65°或115°.
 连结OA、OB,如图,
连结OA、OB,如图,∵PA、PB分别切⊙O于A、B两点,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∴∠AOB=180°-∠APB=180°-50°=130°,
当点C在优弧AB上,则∠ACB=
| 1 |
| 2 |
当点C在劣弧AB上,即C′的位置,则∠AC′B=180°-∠ACB=180°-65°=115°,
即∠ACB为65°或115°.
故答案为65°或115°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理和分类讨论思想的运用.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
在直角坐标系中,O为坐标原点,已知点A(4,3),在坐标轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
| A、2个 | B、4个 | C、6个 | D、8个 |
抛物线y=(x-2)2+3的对称轴是( )
| A、直线x=2 |
| B、直线x=3 |
| C、直线x=-2 |
| D、直线x=-3 |
 如图所示,某工厂A前面有一条笔直的公路,原来有两条路AB,CD可以从工厂A到达公路,经测量AB=6千米,AC=8千米,BC=10千米,现需要修建一条公路,使工厂A到公路的距离最短.请你帮工厂A设计一种方案,并求出最短距离.
如图所示,某工厂A前面有一条笔直的公路,原来有两条路AB,CD可以从工厂A到达公路,经测量AB=6千米,AC=8千米,BC=10千米,现需要修建一条公路,使工厂A到公路的距离最短.请你帮工厂A设计一种方案,并求出最短距离. 如图,已知OA⊥OB,OC⊥OD,O为垂足,若∠AOD=138°,求∠BOC的度数.
如图,已知OA⊥OB,OC⊥OD,O为垂足,若∠AOD=138°,求∠BOC的度数. 如图,已知△ABC∽△DBE.DB=8,AB=6,则S△ABC:S△DBE=
如图,已知△ABC∽△DBE.DB=8,AB=6,则S△ABC:S△DBE=