题目内容
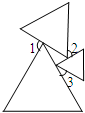三个等边三角形的位置如图所示，若∠1+∠3=122°，则∠2=考点：等边三角形的性质
专题：
分析：先根据图中是三个等边三角形可知三角形各内角等于60°，用∠1，∠2，∠3表示出△ABC各角的度数，再根据三角形内角和定理即可得出结论．
解答：
解：∵图中是三个等边三角形，
∴∠ABC=180°-60°-∠3=120°-∠3，∠ACB=180°-60°-∠2=120°-∠2，
∠BAC=180°-60°-∠1=120°-∠1，
∵∠ABC+∠ACB+∠BAC=180°，
∴120°-∠3+（120°-∠2）+（120°-∠1）=180°，
∴∠1+∠2+∠3=180°．
∵∠1+∠3=122°，则∠2=58度．
故答案为：58．
解：∵图中是三个等边三角形，∴∠ABC=180°-60°-∠3=120°-∠3，∠ACB=180°-60°-∠2=120°-∠2，
∠BAC=180°-60°-∠1=120°-∠1，
∵∠ABC+∠ACB+∠BAC=180°，
∴120°-∠3+（120°-∠2）+（120°-∠1）=180°，
∴∠1+∠2+∠3=180°．
∵∠1+∠3=122°，则∠2=58度．
故答案为：58．
点评：本题考查的是等边三角形的性质，熟知等边三角形各内角均等于60°是解答此题的关键．
练习册系列答案
相关题目
如图，正三角形ABC的边长为2，点A，B在半径为
如图所示，某工厂A前面有一条笔直的公路，原来有两条路AB，CD可以从工厂A到达公路，经测量AB=6千米，AC=8千米，BC=10千米，现需要修建一条公路，使工厂A到公路的距离最短．请你帮工厂A设计一种方案，并求出最短距离．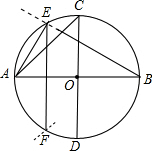
如图，在⊙O中，如果作两条互相垂直的直径AB、CD，那么弦AC是⊙O的内接正方形的一边；如果以点A为圆心，以OA为半径画弧，与⊙O相交于点E，F，那么弦AE、CE、EF分别是⊙O的内接正六边形、正十二边形、正三角形的一边，为什么？
如图，已知OA⊥OB，OC⊥OD，O为垂足，若∠AOD=138°，求∠BOC的度数．在直角坐标系中，O为坐标原点，已知点A（4，3），在坐标轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数共有（ ）
| A、2个 | B、4个 | C、6个 | D、8个 |