题目内容
20.在正方形ABCD中,点E在CD边上,AE的垂直平分线分别交AD、CB于F、G两点,垂足为点H.(1)如图1,求证:AE=FG;
(2)如图2,若AB=9,DE=3,求HG的长.
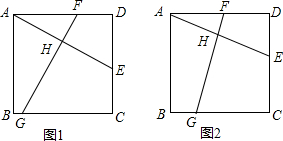
分析 (1)过D点作DN∥FG交BC于点N,交AE于点M,证出四边形FGND是平行四边形,得出DN=FG,由ASA证明△DNC≌△AED,得出DN=AE,即可得出结论;
(2)在Rt△ADE中,由勾股定理求出AE=3$\sqrt{10}$,由三角函数得出tan∠DAE=$\frac{DE}{AD}$=$\frac{1}{3}$,再由三角函数求出FH=$\frac{1}{3}$AH=$\frac{\sqrt{10}}{2}$,即可得出结果.
解答  (1)证明:过D点作DN∥FG交BC于点N,交AE于点M
(1)证明:过D点作DN∥FG交BC于点N,交AE于点M
在正方形ABCD中,AD∥BC,AD=DC,∠ADC=∠C=90°,
则四边形FGND是平行四边形,
∴DN=FG,
∵FG垂直平分AE,
∴∠FHA=90°
∵DN∥FG,
∴∠DMA=∠FHA=90°,
∴∠NDE+∠AED=90°,
又∵∠DAE+∠AED=90°,
∴∠NDE=∠DAE,
在△DNC和△AED中,$\left\{\begin{array}{l}{∠NDE=∠DAE}&{\;}\\{CD=DA}&{\;}\\{∠C=∠ADC}&{\;}\end{array}\right.$,
∴△DNC≌△AED(ASA),
∴DN=AE,
∴AE=FG;
(2)解:在正方形ABCD中,∠D=90°,AD=9,DE=3
在Rt△ADE中,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{9}^{2}+{3}^{2}}$=3$\sqrt{10}$,tan∠DAE=$\frac{DE}{AD}$=$\frac{3}{9}$=$\frac{1}{3}$,
∴在Rt△AHF中,tan∠FAH=$\frac{FH}{AH}$=$\frac{1}{3}$,
点H为AE中点,AH=HE=$\frac{1}{2}$AE=$\frac{3\sqrt{10}}{2}$,
∴FH=$\frac{1}{3}$AH=$\frac{\sqrt{10}}{2}$,
∴HG=FG-FH=3$\sqrt{10}$-$\frac{\sqrt{10}}{2}$=$\frac{5\sqrt{10}}{2}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、平行四边形的判定与性质、勾股定理.三角函数等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

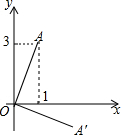 如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )| A. | $\sqrt{10}$ | B. | 3 | C. | 2$\sqrt{2}$ | D. | 1 |
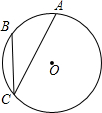 如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )
如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )| A. | π | B. | $\frac{3π}{2}$ | C. | 2π | D. | 3π |
| A. | a≥-2 | B. | a<-2 | C. | a≤-2 | D. | a>-2 |
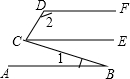 如图,AB∥CE,CE∥DF,则∠BCD等于( )
如图,AB∥CE,CE∥DF,则∠BCD等于( )| A. | ∠2-∠1 | B. | ∠1+∠2 | C. | 180°+∠1-∠2 | D. | 180°+∠2-2∠1 |
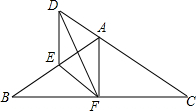 如图,△ABC中,AB=AC,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
如图,△ABC中,AB=AC,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.



 如图,原来是重叠的两个直角三角形,将其中一个三角形沿BC方向平移BE的距离,就得到此图形,则图中阴影部分的面积为32.5.
如图,原来是重叠的两个直角三角形,将其中一个三角形沿BC方向平移BE的距离,就得到此图形,则图中阴影部分的面积为32.5.