题目内容
10．
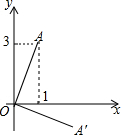如图，已知A（1，3），将线段OA绕原点O顺时针旋转90°后得到OA′，则OA′的长度是（ ）| A． | $\sqrt{10}$ | B． | 3 | C． | 2$\sqrt{2}$ | D． | 1 |
分析 先利用勾股定理计算出OA的长，然后根据旋转的性质即可得到OA′的长度．
解答 解：∵A点坐标为（1，3），
∴OA=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，
∵线段OA绕原点O顺时针旋转90°后得到OA′，
∴OA′=OA=$\sqrt{10}$．
故选A．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
练习册系列答案
全能测控期末小状元系列答案
相关题目
20．下列各组中，是二元一次方程x+2y=3的解的是（ ）
| A． | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=0}\\{y=\frac{2}{3}}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ |
1．
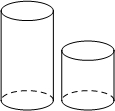图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体的视图说法正确的是（ ）
图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体的视图说法正确的是（ ）| A． | 俯视图相同 | B． | 主视图、俯视图、左视图都相同 | ||
| C． | 左视图相同 | D． | 主视图相同 |
5．
如图为一个几何体三视图，主视图和俯视图都是矩形，则侧面积是（ ）
如图为一个几何体三视图，主视图和俯视图都是矩形，则侧面积是（ ）| A． | 8+4$\sqrt{2}$ | B． | 20+8$\sqrt{2}$ | C． | 16+8$\sqrt{2}$ | D． | 12+4$\sqrt{2}$ |
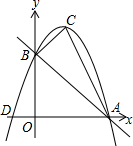如图，已知直线y=-x+3的图象分别交x轴于A点，交y轴于B点，抛物线y=-x2+bx+c经过点A、B两点，并与x轴交于另一点D，顶点为C．
19．
如图中几何体的俯视图是（ ）
如图中几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
