题目内容
12.写出下列不等式的变形依据:(1)若x+2>3,则x>1;
(2)若2x>-3,则x>-$\frac{3}{2}$;
(3)若-3x>2,则x<$-\frac{2}{3}$;
(4)若-$\frac{x}{2}$>5,则x<-10.
分析 (1)根据不等式的性质1,不等式的两边都加(或减)同一个数,不等号的方向不变,可得答案;
(2)根据不等式的性质2,不等式的两边都乘以(或除以)同一个正数,不等号的方向不变,可得答案;
(3)根据不等式的性质3,不等式的两边都乘以(或除以)同一个负数,不等号的方向改变,可得答案;
(4)根据不等式的性质3,不等式的两边都乘以(或除以)同一个负数,不等号的方向改变,可得答案.
解答 解:(1)若x+2>3,则x>1,根据不等式的性质1,不等式的两边都减2;
(2)若2x>-3,则x>-$\frac{3}{2}$,根据不等式的性质2,不等式的两边都除以2;
(3)若-3x>2,则x<$-\frac{2}{3}$,根据不等式的性质3,不等式的两边都除以-3;
(4)若-$\frac{x}{2}$>5,则x<-10根据不等式的性质3,不等式的两边都乘以-2.
点评 本题考查了不等式的性质,熟记不等式的性质是解题关键,注意不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.某学校九年级8班10名学生积极奉献爱心,自发组织捐款,支援贫困山区儿童,若他们捐款的数额分别是(单位:元):10,15,20,10,5,15,10,5,10,5,则这组捐款的众数和中位数分别是( )
| A. | 5元、10元 | B. | 15元、5元 | C. | 10元、15元 | D. | 10元、10元 |
17. 如图所示,几何体的左视图是( )
如图所示,几何体的左视图是( )
 如图所示,几何体的左视图是( )
如图所示,几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
4.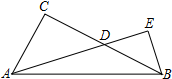 如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )
如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )
 如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )
如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
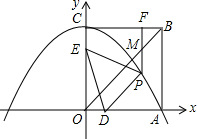 如图,边长为4的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含点A,C),过P点作PF⊥BC于点F,点D,E的坐标分别为D(1,0),E(0,3).连接DE,PD,PE,OB.
如图,边长为4的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含点A,C),过P点作PF⊥BC于点F,点D,E的坐标分别为D(1,0),E(0,3).连接DE,PD,PE,OB.