题目内容
9.若不等式组$\left\{\begin{array}{l}{x+a≥0}\\{4-2x>x-2}\end{array}\right.$有解,则实数a的取值范围是( )| A. | a≥-2 | B. | a<-2 | C. | a≤-2 | D. | a>-2 |
分析 先解不等式组,然后根据题意可得a>-2,由此求得a的取值.
解答 解:$\left\{\begin{array}{l}{x+a≥0}\\{4-2x>x-2}\end{array}\right.$,
解不等式x+a≥0得,x≥-a,
由不等式4-2x>x-2得,x<2,
∵不等式组:不等式组$\left\{\begin{array}{l}{x+a≥0}\\{4-2x>x-2}\end{array}\right.$有解,
∴a>-2,
故选D.
点评 本题考查了不等式组有解的条件,属于中档题.

练习册系列答案
相关题目
19. 如图中几何体的俯视图是( )
如图中几何体的俯视图是( )
 如图中几何体的俯视图是( )
如图中几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
17. 如图所示,几何体的左视图是( )
如图所示,几何体的左视图是( )
 如图所示,几何体的左视图是( )
如图所示,几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
4.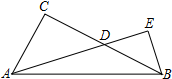 如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )
如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )
 如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )
如图,在△ABC中,∠C=90°,点D是BC边上一动点,过点B作BE⊥AD交AD的延长线于E.若AC=6,BC=8,则$\frac{DE}{AD}$的最大值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
18.下列命题不正确的是( )
| A. | 0是整式 | B. | x=0是一元一次方程 | ||
| C. | (x+1)(x-1)=x2+x是一元二次方程 | D. | $\sqrt{4}$是二次根式 |
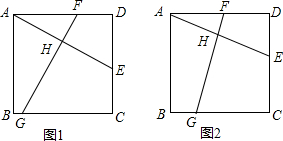
 如图是将正方体切去一个角后形成的几何体,则其主(正)视图为( )
如图是将正方体切去一个角后形成的几何体,则其主(正)视图为( )



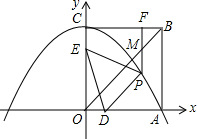 如图,边长为4的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含点A,C),过P点作PF⊥BC于点F,点D,E的坐标分别为D(1,0),E(0,3).连接DE,PD,PE,OB.
如图,边长为4的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含点A,C),过P点作PF⊥BC于点F,点D,E的坐标分别为D(1,0),E(0,3).连接DE,PD,PE,OB.