��Ŀ����
8���Ķ����ϣ��ش����⣺��1���й��Ŵ���ѧ����ͼ1�������㾭�����������ļ��أ����������������ģ������壮������仰����˼�ǣ������ֱ����������ֱ�DZ�Ϊ3��4ʱ����ôб�ߵij�Ϊ5�������������ر����ˣ���Rt��ABC�У������C=90�㣬BC=a��AC=b��AB=c����ôa��b��c����֮���������ϵ�ǣ�a2+b2=c2��
��2���������������ϵ���ҹ�������ѧ����ˬ���ݡ���ˬ��ͼ������ͼ2�������ɰ˸�ȫ��ֱ��������Χ�ɵ�һ�������Σ������������������֤�����ο���ˬ��˼·���������֤�����̲���������
֤������S��ABC=$\frac{1}{2}ab$��S������ABCD=c2��
S������MNPQ=��a+b��2��
�֡�������MNPQ�����=�ĸ�ȫ��ֱ�������ε����+������AEDB�������
�ࣨa+b��2=$4��\frac{1}{2}ab+{c}^{2}$��
������a2+2ab+b2=2ab+c2��
��a2+b2=c2��
��3����ͼ3���Ѿ���ABCD�۵���ʹ��C���A�غϣ��ۺ�ΪEF�����AB=4��BC=8����BE�ij���
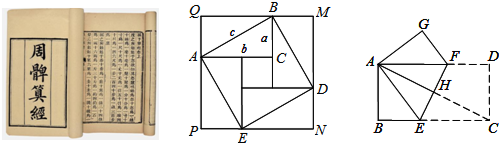
���� ��1�����ݹ��ɶ�����ɣ�
��2���������⡢���ͼ�Σ�������ȫƽ����ʽ���м��㼴�ɣ�
��3�����ݷ��۱任���ص㡢���ݹ��ɶ����г����̣��ⷽ�̼��ɣ�
��� �⣺��1����Rt��ABC�У���C=90�㣬BC=a��AC=b��AB=c��
�ɹ��ɶ����ã�a2+b2=c2��
�ʴ�Ϊ��a2+b2=c2��
��2����S��ABC=$\frac{1}{2}ab$��S������ABCD=c2��
S������MNPQ=��a+b��2��
�֡������ε����=�ĸ�ȫ��ֱ�������ε���������+������AEDB�������
�ࣨa+b��2=$4��\frac{1}{2}ab+{c}^{2}$��
�����ã�a2+2ab+b2=2ab+c2��
��a2+b2=c2��
�ʴ�Ϊ����a+b��2�������ε�������ĸ�ȫ��ֱ�������ε���������+������AEDB�������a2+b2=c2��
��3����BE=x����EC=8-x��
���۵������ʿ�֪��AE=EC=8-x��
��Rt��ABE��AE2=AB2+BE2��
��8-x��2=42+x2��
��ã�x=3��
��BE�ij�Ϊ3��
���� ���⿼����������κ;��ε����ʡ����ɶ��������۱任�����ʣ���ȷ����ɶ���������������ν��˼���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
18��ƽ����3�������غϵ�ֱ�߽���һ�㣬���жԶ����У�������
| A�� | 4�� | B�� | 5�� | C�� | 6�� | D�� | 7�� |
19��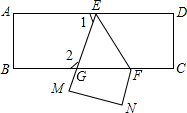 ��ͼ��֪����һ�ų�����ֽƬABCD��EF�۵���ED��BC�Ľ���ΪG��D��C�ֱ���M��N��λ���ϣ�����EFG=55�㣬���1�͡�2�Ķ�����
��ͼ��֪����һ�ų�����ֽƬABCD��EF�۵���ED��BC�Ľ���ΪG��D��C�ֱ���M��N��λ���ϣ�����EFG=55�㣬���1�͡�2�Ķ�����
 ��ͼ��֪����һ�ų�����ֽƬABCD��EF�۵���ED��BC�Ľ���ΪG��D��C�ֱ���M��N��λ���ϣ�����EFG=55�㣬���1�͡�2�Ķ�����
��ͼ��֪����һ�ų�����ֽƬABCD��EF�۵���ED��BC�Ľ���ΪG��D��C�ֱ���M��N��λ���ϣ�����EFG=55�㣬���1�͡�2�Ķ�����
3��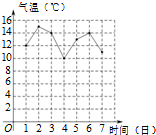 ��ͼ��ij��10��1����7��һ���ڡ���ƽ�����±仯ͳ��ͼ���������������У���������λ���ֱ��ǣ�������
��ͼ��ij��10��1����7��һ���ڡ���ƽ�����±仯ͳ��ͼ���������������У���������λ���ֱ��ǣ�������
 ��ͼ��ij��10��1����7��һ���ڡ���ƽ�����±仯ͳ��ͼ���������������У���������λ���ֱ��ǣ�������
��ͼ��ij��10��1����7��һ���ڡ���ƽ�����±仯ͳ��ͼ���������������У���������λ���ֱ��ǣ�������| A�� | 13��13 | B�� | 14��14 | C�� | 13��14 | D�� | 14��13 |
13���������й�Ϸ����Ա���ϵĻ滭��������̨�ݳ�ʱ�Ļ�ױ���ͣ�����������������Ը�������������а�������ͼƬ�У������ȡһ��Ϊ �ĸ����ǣ�������
�ĸ����ǣ�������

 �ĸ����ǣ�������
�ĸ����ǣ�������
| A�� | $\frac{1}{3}$ | B�� | $\frac{5}{8}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{3}{8}$ |
20����2015���^ѧ���𣬱���110 000����һ����ͨ���������г���ʵ�����������ƽ̨������ѡ�Σ��μӡ������Կ�ѧʵ������γ̣���110 000�ÿ�ѧ��������ʾӦΪ��������
| A�� | 11��104 | B�� | 1.1��105 | C�� | 1.1��106 | D�� | 0.11��106 |
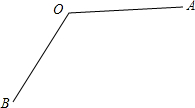 ��1���ó߹���ͼ�ķ�����������AOB��ƽ����OC��������ͼ�ۼ�����Ҫ��д����������
��1���ó߹���ͼ�ķ�����������AOB��ƽ����OC��������ͼ�ۼ�����Ҫ��д����������