题目内容
5.菱形中某两个角的和是90°,周长是12,则菱形的面积是( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\frac{7\sqrt{2}}{2}$ | D. | $\frac{9\sqrt{2}}{2}$ |
分析 直接利用菱形的性质得出其内角度数,进而利用锐角三角函数关系得出AE的长,即可得出菱形的面积.
解答 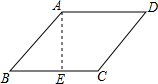 解:如图所示:过点A作AE⊥BC于点E,
解:如图所示:过点A作AE⊥BC于点E,
∵菱形中某两个角的和是90°,
∴只有一组对角和为90°,如图所示:∠B+∠D=90°,
则∠B=45°,
∵菱形的周长为:12,
∴AB=3,
∴AE=AB•sin45°=$\frac{3\sqrt{2}}{2}$,
∴菱形的面积是:AE•BC=3×$\frac{3\sqrt{2}}{2}$=$\frac{9\sqrt{2}}{2}$.
故选:D.
点评 此题主要考查了菱形的性质以及锐角三角函数关系,得出菱形一边上的高是解题关键.

练习册系列答案
相关题目
20.从2015年秋季学期起,北京110 000名初一新生通过“北京市初中实践活动管理服务平台”进行选课,参加“开放性科学实践活动”课程.将110 000用科学记数法表示应为( )
| A. | 11×104 | B. | 1.1×105 | C. | 1.1×106 | D. | 0.11×106 |
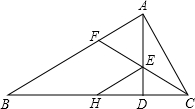 如图,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,过E作EH∥AB,交BC于H,求证:AF=EH.
如图,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,过E作EH∥AB,交BC于H,求证:AF=EH.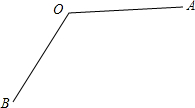 (1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);
(1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);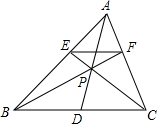 如图,△ABC中,E、F在AB、AC上,EF∥BC,BF、CE交于点P,延长AP交BC于点D,求证:BD=CD.
如图,△ABC中,E、F在AB、AC上,EF∥BC,BF、CE交于点P,延长AP交BC于点D,求证:BD=CD.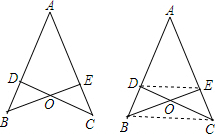 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.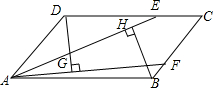 如图,点E,F分别在?ABCD的边DC,CB上,且AE=AF,DG⊥AF,BH⊥AE,垂足分别为G,H.求证:DG=BH.
如图,点E,F分别在?ABCD的边DC,CB上,且AE=AF,DG⊥AF,BH⊥AE,垂足分别为G,H.求证:DG=BH.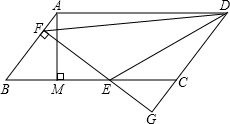 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.