题目内容
4.已知实数a、b满足条件:a2+4b2-a+4b+$\frac{5}{4}$=0,求-ab的平方根.分析 利用配方法得到(a-$\frac{1}{2}$)2+(2b+1)2=0,根据非负数的性质得a-$\frac{1}{2}$=0,2b+1=0,解得a=$\frac{1}{2}$,b=-$\frac{1}{2}$,所以-ab=$\frac{1}{4}$,然后根据平方根的定义求解.
解答 解:∵a2+4b2-a+4b+$\frac{5}{4}$=0,
∴a2-a+$\frac{1}{4}$+4b2+4b+1=0,
∴(a-$\frac{1}{2}$)2+(2b+1)2=0,
∴a-$\frac{1}{2}$=0,2b+1=0,
∴a=$\frac{1}{2}$,b=-$\frac{1}{2}$,
∴-ab=$\frac{1}{4}$,
∴-ab的平方根为±$\frac{1}{2}$.
点评 本题考查了配方法的应用:用配方法解一元二次方程;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.也考查了非负数的性质.

练习册系列答案
相关题目
20.从2015年秋季学期起,北京110 000名初一新生通过“北京市初中实践活动管理服务平台”进行选课,参加“开放性科学实践活动”课程.将110 000用科学记数法表示应为( )
| A. | 11×104 | B. | 1.1×105 | C. | 1.1×106 | D. | 0.11×106 |
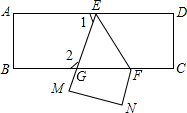 如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数.
如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数.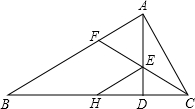 如图,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,过E作EH∥AB,交BC于H,求证:AF=EH.
如图,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,过E作EH∥AB,交BC于H,求证:AF=EH.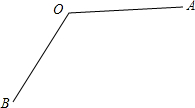 (1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);
(1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);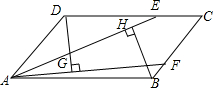 如图,点E,F分别在?ABCD的边DC,CB上,且AE=AF,DG⊥AF,BH⊥AE,垂足分别为G,H.求证:DG=BH.
如图,点E,F分别在?ABCD的边DC,CB上,且AE=AF,DG⊥AF,BH⊥AE,垂足分别为G,H.求证:DG=BH.