题目内容
2.如图,网格中的每个四边形都是菱形,如果格点三角形ABC的面积为S,按照如图所示方式得到的格点三角形A1B1C1的面积是7S,格点三角形A2B2C2的面积是19S,那么格点三角形A3B3C3的面积为37S,如此下去,格点三角形AnBnCn的面积为[(n+1)3-n3]S.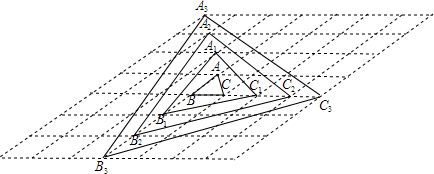
分析 利用已知三角形面积变化得出△AnBnCn的面积为[(n+1)3-n3]S,进而得出答案.
解答 解:已知格点△ABC的面积为S,
格点△A1B1C1的面积是:(23-13)S=7S,
格点△A2B2C2的面积是:(33-23)S=19S,
则格点△A3B3C3的面积是:(43-33)S=37S,
以此类推:格点△AnBnCn的面积为:[(n+1)3-n3]S.
故答案为:37,[(n+1)3-n3]S.
点评 此题主要考查了图形的面积变化规律,根据已知得出图形变化规律是解题关键.

练习册系列答案
相关题目
12.已知a2(b+c)=b2(a+c)=2015,且a,b,c互不相等,则c2(a+b)-2014的值为( )
| A. | 0 | B. | 1 | C. | 2015 | D. | -2015 |
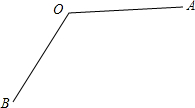 (1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);
(1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);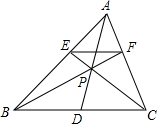 如图,△ABC中,E、F在AB、AC上,EF∥BC,BF、CE交于点P,延长AP交BC于点D,求证:BD=CD.
如图,△ABC中,E、F在AB、AC上,EF∥BC,BF、CE交于点P,延长AP交BC于点D,求证:BD=CD.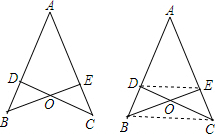 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.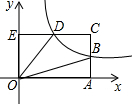 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OECA的边AC于B点,交CE于D点,且B是AC的中点,若四边形ODCB的面积是5,则k=5.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OECA的边AC于B点,交CE于D点,且B是AC的中点,若四边形ODCB的面积是5,则k=5.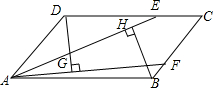 如图,点E,F分别在?ABCD的边DC,CB上,且AE=AF,DG⊥AF,BH⊥AE,垂足分别为G,H.求证:DG=BH.
如图,点E,F分别在?ABCD的边DC,CB上,且AE=AF,DG⊥AF,BH⊥AE,垂足分别为G,H.求证:DG=BH.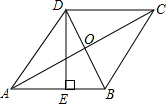 如图,在菱形ABCD中,DE=AO,DE⊥AB,AB=2.
如图,在菱形ABCD中,DE=AO,DE⊥AB,AB=2.