题目内容
13.如图(1),点E为矩形ABCD边AD上一点,点P,Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图(2),则下列正确的是( )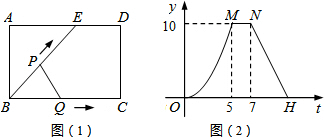
| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |
分析 由图2可知,在点(5,10)至点(7,10)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下:
(1)在BE段,BP=BQ;持续时间5s,则BE=BC=5;y是t的二次函数;
(2)在ED段,y=10是定值,持续时间2s,则ED=2;
(3)在DC段,y持续减小直至为0,y是t的一次函数.
解答 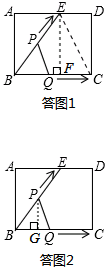 解:(1)分析函数图象可知,BC=5cm,ED=2cm,故AE=AD-ED=BC-ED=5-2=3cm,故A错误;
解:(1)分析函数图象可知,BC=5cm,ED=2cm,故AE=AD-ED=BC-ED=5-2=3cm,故A错误;
(2)如答图1所示,连接EC,过点E作EF⊥BC于点F,
由函数图象可知,BC=BE=5cm,S△BEC=10=$\frac{1}{2}$BC•EF=$\frac{1}{2}$×5×EF,∴EF=4,
∴sin∠EBC=$\frac{EF}{BE}=\frac{4}{5}$,故B正确;
(3)如答图2所示,当0<t≤5时,
过点P作PG⊥BQ于点G,
∵BQ=BP=t,
∴y=S△BPQ=$\frac{1}{2}$BQ•PG=$\frac{1}{2}$BQ•BP•sin∠EBC=$\frac{1}{2}$t•t•$\frac{4}{5}$=$\frac{2}{5}$t2(0<t≤5),故C错误;
(4)sin∠EBC=$\frac{EF}{BE}=\frac{4}{5}$,AE=3cm,所以AB=CD=4cm,所以t=11时,P到达C点停止运动,故D错误.
故选:B.
点评 本题考查动点问题的函数图象,需要结合几何图形与函数图象,认真分析动点的运动过程.突破点在于正确判断出BC=BE=5cm.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
8.某学校组织学生到距离学校6千米的科技馆去参观,小华因事没能乘上学校的包车,于是准备在学校门口改乘出租车去科技馆,出租车标注收费有两种类型,如表:
(1)设出租车行驶的里程为x千米(x≥3且x取正整数),分别写出两种类型的总收费y(用含x的代数式表示);
(2)小华身上仅有10元,他乘出租车到科技馆车费够不够?请说明理由.
| 里程 | 甲类收费(元) | 乙类收费(元) |
| 3千米以下(包含3千米) | 5.00 | 6.00 |
| 3千米以上,每增加1千米 | 1.60 | 1.30 |
(2)小华身上仅有10元,他乘出租车到科技馆车费够不够?请说明理由.
 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示. 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.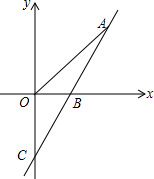 如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.
如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.
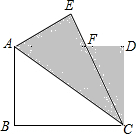 如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.
如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.