题目内容
18.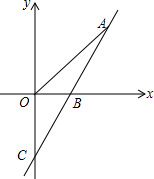 如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.
如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.(1)求B点的坐标和k的值;
(2)当△AOB的面积是4时,求A点在第一象限的坐标;
(3)在(2)的条件下,在x轴上是否存在一点P,使△POA是等腰三角形?若存在,请直接写出满足条件的所有P点的坐标;若不存在,请说明理由.
分析 (1)对于直线解析式,令x=0求出y的值,确定出C的长,进而求出OC的长,根据OC=2OB求出OB的长,确定出B坐标,代入直线解析式求出k的值即可;
(2)三角形AOB以OB为底边,A纵坐标为高,表示出面积,根据面积为4求出A的纵坐标,代入直线解析式求出横坐标,即可确定出A的坐标;
(3)在(2)的条件下,在x轴上存在一点P,使△POA是等腰三角形,分三种情况考虑:①若OA=OP1时,△OP1A为等腰三角形;②若AP2=OP2时,△OP2A为等腰三角形;③若OA=AP3时,△OAP3为等腰三角形,分别求出P坐标即可.
解答 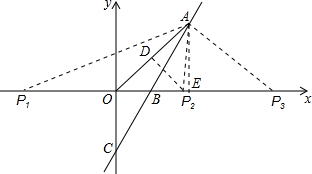 解:(1)对于直线y=kx-2,
解:(1)对于直线y=kx-2,
令x=0,得到y=-2,即C(0,-2),
∵OC=2OB,OC=2,
∴OB=1,即B(1,0),
把B(1,0)代入直线解析式得:k=2;
(2)∵S△ABC=$\frac{1}{2}$OB•yA=4,OB=1,
∴yA=8,
把y=8代入y=2x-2中,得x=5,
则A的坐标为(5,8);
(3)在(2)的条件下,在x轴上存在一点P,使△POA是等腰三角形,
如图所示,分三种情况考虑:
①若OA=OP1时,△OP1A为等腰三角形,
根据勾股定理得:OA=$\sqrt{{5}^{2}+{8}^{2}}$=$\sqrt{89}$,
∴OP1=$\sqrt{89}$,即P1坐标为(-$\sqrt{89}$,0);
②若AP2=OP2时,△OP2A为等腰三角形,DP2垂直平分线段OA,
∵直线OA解析式为y=$\frac{8}{5}$x,D坐标为($\frac{5}{2}$,4),
∴直线P2D解析式为y-4=-$\frac{5}{8}$(x-$\frac{5}{2}$),
令y=0,得到x=8.9,即P2(8.9,0);
③若OA=AP3时,△OAP3为等腰三角形,
过A作AE⊥x轴,可得OE=P3E=5,即OP3=10,此时P3(10,0),
综上,在(2)的条件下,在x轴上存在一点P,使△POA是等腰三角形,P的坐标为(-$\sqrt{89}$,0)或(8.9,0)或(10,0).
点评 此题属于一次函数综合题,涉及的知识有:待定系数法求一次函数解析式,一次函数与坐标轴的交点,等腰三角形的性质,利用了分类讨论的思想,熟练掌握待定系数法是解本题的关键.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |
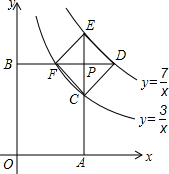 如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.
如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.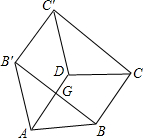 如图,四边形ABCD和四边形AB′C′D都是菱形,且∠BAD=∠B′AD,连接BB′、CC′,BB′与AD相交于点G.
如图,四边形ABCD和四边形AB′C′D都是菱形,且∠BAD=∠B′AD,连接BB′、CC′,BB′与AD相交于点G.
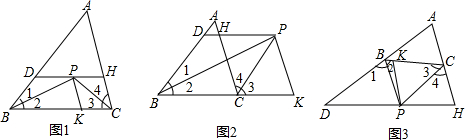
 如图所示,已知CD是△ABC中∠ACB的外角平分线,请说明:∠BAC>∠B.
如图所示,已知CD是△ABC中∠ACB的外角平分线,请说明:∠BAC>∠B.