题目内容
3.从地面竖直向上抛出一小球,小球的高度h(米)与小球运动时间t(秒)的关系式是h=30t-5t2,小球运动中的最大高度是45米.分析 首先理解题意,先把实际问题转化成数学问题后,知道解此题就是求出h=30t-5t2的顶点坐标即可.
解答 解:h=-5t2+30t
=-5(t2-6t+9)+45
=-5(t-3)2+45,
∵a=-5<0,
∴图象的开口向下,有最大值,
当t=3时,h最大值=45.
故答案为:45.
点评 本题考查了二次函数的应用.解此题的关键是把实际问题转化成数学问题,利用二次函数的性质就能求出结果,求抛物线顶点坐标的常用方法是把一般式配方为顶点式或用顶点坐标公式计算.

练习册系列答案
相关题目
13.如图(1),点E为矩形ABCD边AD上一点,点P,Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图(2),则下列正确的是( )
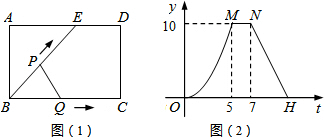

| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |
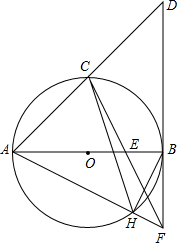 如图,AB是⊙O的直径,点C是$\widehat{AB}$的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
如图,AB是⊙O的直径,点C是$\widehat{AB}$的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.