题目内容
2.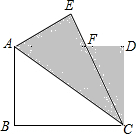 如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.
如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.
分析 首先根据翻折变换的性质,可得AE=AB=6,CE=BC=8,∠AEC=90°,所以S△ACE=6×8÷2=24,然后设DF=x,CF=y,根据勾股定理,求出x、y的值,再根据三角形的面积的求法,求出三角形CDF的面积;最后用三角形ACE的面积加上三角形CDF的面积,求出折叠后所成的图形覆盖的面积(阴影部分的面积)是多少即可.
解答 解:如图1, ,
,
根据翻折变换的性质,可得
AE=AB=6,CE=BC=8,∠AEC=90°,
∴S△ACE=6×8÷2=24,
设DF=x,CF=y,
则AF=8-x,EF=8-y,
∴$\left\{\begin{array}{l}{{x}^{2}+36{=y}^{2}}\\{{(8-y)}^{2}+36{=(8-x)}^{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=1.75}\\{y=6.25}\end{array}\right.$
∴S△CDF=6×1.75÷2=5.25,
∴折叠后所成的图形覆盖的面积(阴影部分的面积)是:
24+5.25=29.25.
故答案为:29.25.
点评 (1)此题主要考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
(2)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.

练习册系列答案
相关题目
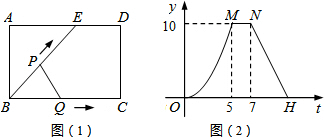
13.如图(1),点E为矩形ABCD边AD上一点,点P,Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图(2),则下列正确的是( )

| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |
12.某手机专营店代理销售A、B两种型号手机.手机的进价、售价如下表:
(1)第一个月:用54000元购进A、B两种型号的手机,全部售完后获利9450元,求第一个月购进A、B两种型号手机的数量;
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?
| 型 号 | A | B |
| 进 价 | 1800元/部 | 1500元/部 |
| 售 价 | 2070元/部 | 1800元/部 |
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?
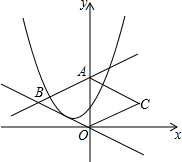 如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,
如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,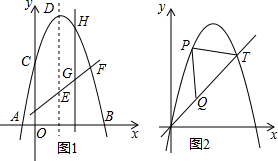
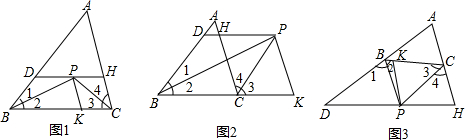
 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.
如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.