题目内容
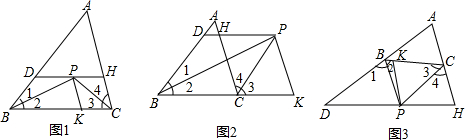
5.如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E.(1)若PB平分∠ABO,求证:AP=CD;
(2)若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)

分析 (1)求出∠3=∠4,∠BOP=∠PED=90°,∠ABP=∠4,求出△ABP≌△CPD,即可得出答案;
(2)设OP=CP=x,求出AP=3x,CD=$\sqrt{2}$x,即可得出答案.
解答 解:(1)如图1,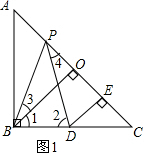
∵PB=PD,
∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,
∴∠1=45°,
∴∠1=∠C=45°,
∵∠3=∠PBC-∠1,∠4=∠2-∠C,
∴∠3=∠4,
∵BP平分∠ABO,
∴∠ABP=∠3,
∴∠ABP=∠4,
在△ABP和△CPD中
$\left\{\begin{array}{l}{∠A=∠C}\\{∠ABP=∠4}\\{PB=PD}\end{array}\right.$
∴△ABP≌△CPD(AAS),
∴AP=CD.
(2)CD′与AP′的数量关系是CD′=$\frac{\sqrt{2}}{3}$AP′.如图2,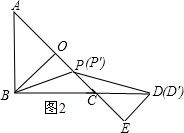
理由是:设OP=PC=x,则AO=OC=2x=BO,
则AP=2x+x=3x,
由△OBP≌△EPD,得BO=PE,
PE=2x,CE=2x-x=x,
∵∠E=90°,∠ECD=∠ACB=45°,
∴DE=x,由勾股定理得:CD=$\sqrt{2}$x,
即AP=3x,CD=$\sqrt{2}$x,
∴CD′与AP′的数量关系是CD′=$\frac{\sqrt{2}}{3}$AP′.
点评 本题考查了全等三角形的性质和判定,等腰直角三角形性质,等腰三角形性质等知识点的综合应用,主要考查学生的推理和计算能力.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
13.如图(1),点E为矩形ABCD边AD上一点,点P,Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图(2),则下列正确的是( )
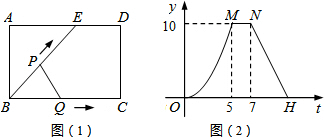

| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |

 如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,
如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC, 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.
如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.