题目内容
3.某大学生利用暑假社会实践参与了一家网店经营,该网店以每个20元的价格购进900个某新型商品.第一周以每个35元的价格售出300个,第二周若按每个35元的价格销售仍可售出300个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个).(1)若第二周降低价格1元售出,则第一周,第二周分别获利多少元?
(2)若第二周单价降低x元销售一周后,商店对剩余商品清仓处理,以每个15元的价格全部售出,如果这批商品计划获利9500元,问第二周每个商品的单价应降低多少元?
分析 (1)根据利润=每个的利润×销售量列式计算即可求解;
(2)设第二周每个商品的单价应降低x元,根据这批商品计划获利9500元建立方程,解方程即可.
解答 解:(1)第一周获利:300×(35-20)=4500(元);
第二周获利:(300+50)×(35-1-20)=4900(元);
(2)根据题意,得:4500+(15-x)(300+50x)-5(900-300-300-50x)=9500,
即:x2-14x+40=0,
解得:x1=4,x2=10,
当x=10时,300+50x=300+500=800,300+800=1100>900(不合题意舍去).
答:第二周每个商品的销售价格应降价4元.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
13.如图(1),点E为矩形ABCD边AD上一点,点P,Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图(2),则下列正确的是( )
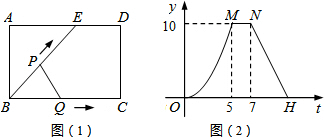

| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |
12.某手机专营店代理销售A、B两种型号手机.手机的进价、售价如下表:
(1)第一个月:用54000元购进A、B两种型号的手机,全部售完后获利9450元,求第一个月购进A、B两种型号手机的数量;
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?
| 型 号 | A | B |
| 进 价 | 1800元/部 | 1500元/部 |
| 售 价 | 2070元/部 | 1800元/部 |
(2)第二个月:计划购进A、B两种型号手机共34部,且不超出第一个月购进A、B两种型号的手机总费用,则A型号手机最多能购多少部?
 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.
如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.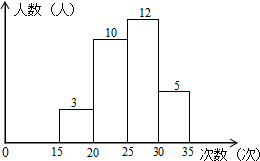 某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在15~20之间的频率为0.1.
某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在15~20之间的频率为0.1. 如图所示,已知CD是△ABC中∠ACB的外角平分线,请说明:∠BAC>∠B.
如图所示,已知CD是△ABC中∠ACB的外角平分线,请说明:∠BAC>∠B.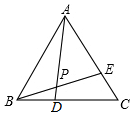 如图,△ABC是等边三角形,点D、E分别是BC、AC边上的两点,其中BD=CE,连接AD、BE交于点P
如图,△ABC是等边三角形,点D、E分别是BC、AC边上的两点,其中BD=CE,连接AD、BE交于点P