题目内容
4. 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
分析 (1)设y=kx+b,则由图象可求得k,b,从而得出y与x之间的函数关系式,并写出x的取值范围80≤x≤160;
(2)设公司第一年获利S万元,则可表示出S=-$\frac{1}{10}$(x-150)2-200≤-200,则第一年公司亏损了,当产品售价定为150元/件时,亏损最小,最小亏损为200万元;
(3)假设两年共盈利790万元,则(x-50)(-$\frac{1}{10}$x+25)+(-200)=790,解得x的值在80≤x≤160内.
解答 解:(1)设y=kx+b.由图象可得:$\left\{\begin{array}{l}{80k+b=17}\\{160k+b=9}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=25}\end{array}\right.$.
所以y=-$\frac{1}{10}$x+25,
故x的取值范围是80≤x≤160.
(2)设该公司第一年获利S万元,则
S=(x-50)×y-1200=(x-50)(-$\frac{1}{10}$x+25)-1200
=-$\frac{1}{10}$x2+30x-2450
=-$\frac{1}{10}$(x-150)2-200≤-200,
所以第一年公司是亏损,且当亏损最小时的产品售价为150元/件.
(3)由题意可列方程(x-50)(-$\frac{1}{10}$x+25)+(-200)=790,
解得:x1=140,x2=160.
两个x的值都在80≤x≤160内,
所以第二年售价是140元/件或160/件.
点评 本题是一道一次函数的综合题,考查了二次函数的应用,还考查了用待定系数法求一次函数的解析式.

练习册系列答案
相关题目
13.如图(1),点E为矩形ABCD边AD上一点,点P,Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发ts时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图(2),则下列正确的是( )
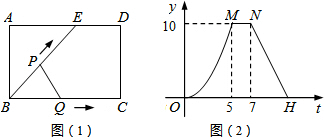

| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |
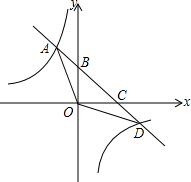 如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=$\frac{m}{x}$与直线y2=-x+b交于A,D两点,直线y2=-x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.
如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=$\frac{m}{x}$与直线y2=-x+b交于A,D两点,直线y2=-x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.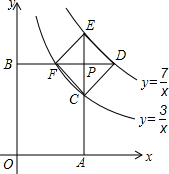 如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.
如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.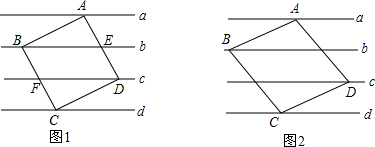
 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.
如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.