题目内容
15.(1)计算:2(x+y)(x-y)-(x+y)2;(2)解方程:$\frac{x}{x-2}+1=\frac{4}{x-2}$;
(3)先化简,再求值:$\frac{{{x^2}-4x+4}}{2x}÷\frac{{{x^2}-2x}}{x^2}+\frac{1}{2}$,在0,1,2三个数中选一个合适的数并代入求值.
分析 (1)先利用平方差公式和完全平方公式展开,然后合并即可;
(2)方程两边同乘以x-2得到整式方程,解得x=3,然后进行检验确定原方程的解;
(3)先把分子分母因式分解,再把除法运算化为乘法运算,然后约分后合并得到原式=$\frac{x-1}{2}$,由于x=0或x=2时,原分式无意义,则把x=0代入计算即可.
解答 解:(1)原式=2x2-2y2-(x2+2xy+y2)
=2x2-2y2-x2-2xy-y2
=x2-3y2-2xy;
(2)去分母得x+x-2=4,
解得x=3,
检验:x=3时,x-2≠0,则x=2是原方程的解,
所以原方程的解为x=3;
(3)原式=$\frac{(x-2)^{2}}{2x}$•$\frac{{x}^{2}}{x(x-2)}$+$\frac{1}{2}$
=$\frac{x-2}{2}$+$\frac{1}{2}$
=$\frac{x-1}{2}$,
当x=1时,原式=$\frac{1-1}{2}$=0.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了解分式方程.

练习册系列答案
相关题目
5.线段a、b、c的长度分别如下,能够以a、b、c为边长构成直角三角形的一组是( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
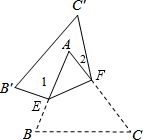 如图,把△ABC沿EF对折,折叠后的图形如图所示.若∠A=60°,∠1=96°,则∠2的度数为24°.
如图,把△ABC沿EF对折,折叠后的图形如图所示.若∠A=60°,∠1=96°,则∠2的度数为24°. 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2),点B的坐标为(-4,5),点C的坐标为(-5,3).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2),点B的坐标为(-4,5),点C的坐标为(-5,3).