题目内容

3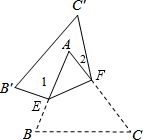．如图，把△ABC沿EF对折，折叠后的图形如图所示．若∠A=60°，∠1=96°，则∠2的度数为24°．

分析 首先根据三角形内角和定理可得∠AEF+∠AFE=120°，再根据邻补角的性质可得∠FEB+∠EFC=360°-120°=240°，再根据由折叠可得：∠B′EF+∠EFC′=∠FEB+∠EFC=240°，然后计算出∠1+∠2的度数，进而得到答案．

解答 解：∵∠A=60°，
∴∠AEF+∠AFE=180°-60°=120°．
∴∠FEB+∠EFC=360°-120°=240°．
∵由折叠可得：∠B′EF+∠EFC′=∠FEB+∠EFC=240°．
∴∠1+∠2=240°-120°=120°．
∵∠1=96°，
∴∠2=120°-96°=24°．
故答案为：24°．

点评 本题主要考查的是翻折的性质、三角形的内角和定理、求得∠1+∠2=120°是解题的关键．

练习册系列答案
相关题目
13．已知x=-1是方程ax=3a+10的解，则a=-2.5．
14．在$-\frac{3}{8}$，0，-30，$\frac{22}{5}$，+20，π，-2.6这7个数中，整数有0，-30，+20，负分数有$-\frac{3}{8}$，-2.6．
11．方程$\frac{1}{2}x+1=0$的解为x=-2．
18．去年四月份中国汽车销售总量为1530000辆，则1530000用科学记数法表示为（　　）
A．153×104B．0.153×107C．1.53×106D．1.53×107
8．观察下列算式：31=3，32=9，33=27，34=81，35=243，36=729，37=2187，38=6561，…
根据上述算式中的规律，你认为32016的末位数字是（　　）
A．3B．9C．7D．1
15．（1）计算：2（x+y）（x-y）-（x+y）2；
（2）解方程：$\frac{x}{x-2}+1=\frac{4}{x-2}$；
（3）先化简，再求值：$\frac{{{x^2}-4x+4}}{2x}÷\frac{{{x^2}-2x}}{x^2}+\frac{1}{2}$，在0，1，2三个数中选一个合适的数并代入求值．
12．观察规律：
$\begin{array}{l}\frac{1}{{\sqrt{2}+1}}=\frac{{\sqrt{2}-1}}{{（{\sqrt{2}+1}）（{\sqrt{2}-1}）}}=\frac{{\sqrt{2}-1}}{2-1}=\sqrt{2}-1\end{array}\begin{array}{l}$
$\frac{1}{{\sqrt{3}+\sqrt{2}}}=\frac{{\sqrt{3}-\sqrt{2}}}{{（{\sqrt{3}+\sqrt{2}}）（{\sqrt{3}-\sqrt{2}}）}}=\frac{{\sqrt{3}-\sqrt{2}}}{3-2}=\sqrt{3}-\sqrt{2}\end{array}$
同理可得：$\begin{array}{l}\frac{1}{{\sqrt{4}+\sqrt{3}}}=\sqrt{4}-\sqrt{3}\end{array}$
依照上述规律，则：$\frac{1}{{\sqrt{11}+\sqrt{10}}}$=$\sqrt{11}$-$\sqrt{10}$； $\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$=$\sqrt{n+1}$-$\sqrt{n}$（n≥1的整数）；
$（{\frac{1}{{\sqrt{2}+1}}+\frac{1}{{\sqrt{3}+\sqrt{2}}}+\frac{1}{{\sqrt{4}+\sqrt{3}}}+…+\frac{1}{{\sqrt{2016}+\sqrt{2015}}}}）（{\sqrt{2016}+1}）$=2015．
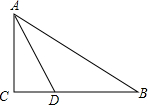4．已知，在△ABC中，AD是角平分线，AD=BD，AB=2AC，求证：△ACB是直角三角形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网