题目内容
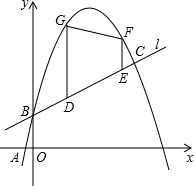 如图,已知一次函数y1=
如图,已知一次函数y1=| 1 |
| 2 |
| 5 |
(1)求二次函数的最大值;
(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程(1+
| 1 |
| a-1 |
| 3 |
| x-3 |
(3)若点F、G在图象C′上,长度为
| 5 |
考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)首先利用待定系数法求出二次函数解析式,然后求出其最大值;
(2)联立y1与y2,求出点C的坐标为C(
,
),因此使y2>y1成立的x的取值范围为0<x<
,得s=1+2+3=6;将s的值代入分式方程,求出a的值;
(3)第1步:首先确定何时四边形DEFG的面积最大.
如答图1,四边形DEFG是一个梯形,将其面积用含有未知数的代数式表示出来,这个代数式是一个二次函数,根据其最值求出未知数的值,进而得到面积最大时点D、E的坐标;
第2步:利用几何性质确定PD+PE最小的条件,并求出点P的坐标.
如答图2,作点D关于x轴的对称点D′,连接D′E,与x轴交于点P.根据轴对称及两点之间线段最短可知,此时PD+PE最小.利用待定系数法求出直线D′E的解析式,进而求出点P的坐标.
(2)联立y1与y2,求出点C的坐标为C(
| 7 |
| 2 |
| 11 |
| 4 |
| 7 |
| 2 |
(3)第1步:首先确定何时四边形DEFG的面积最大.
如答图1,四边形DEFG是一个梯形,将其面积用含有未知数的代数式表示出来,这个代数式是一个二次函数,根据其最值求出未知数的值,进而得到面积最大时点D、E的坐标;
第2步:利用几何性质确定PD+PE最小的条件,并求出点P的坐标.
如答图2,作点D关于x轴的对称点D′,连接D′E,与x轴交于点P.根据轴对称及两点之间线段最短可知,此时PD+PE最小.利用待定系数法求出直线D′E的解析式,进而求出点P的坐标.
解答:解:(1)∵二次函数y2=-x2+mx+b经过点B(0,1)与A(2-
,0),
∴
,
解得
∴l:y1=
x+1;
C′:y2=-x2+4x+1.
∵y2=-x2+4x+1=-(x-2)2+5,
∴ymax=5;
(2)联立y1与y2得:
x+1=-x2+4x+1,解得x=0或x=
,
当x=
时,y1=
×
+1=
,
∴C(
,
).
使y2>y1成立的x的取值范围为0<x<
,
∴s=1+2+3=6.
代入方程得(1+
)6+
=0
解得a=
;
(3)∵点D、E在直线l:y1=
x+1上,
∴设D(p,
p+1),E(q,
q+1),其中q>p>0.
如答图1,过点E作EH⊥DG于点H,则EH=q-p,DH=
(q-p).

在Rt△DEH中,由勾股定理得:EH2+DH2=DE2,即(q-p)2+[
(q-p)]2=(
)2,
解得q-p=2,即q=p+2.
∴EH=2,E(p+2,
p+2).
当x=p时,y2=-p2+4p+1,
∴G(p,-p2+4p+1),
∴DG=(-p2+4p+1)-(
p+1)=-p2+
p;
当x=p+2时,y2=-(p+2)2+4(p+2)+1=-p2+5,
∴F(p+2,-p2+5),
∴EF=(-p2+5)-(
p+2)=-p2-
p+3.
S四边形DEFG=
(DG+EF)•EH=
[(-p2+
p)+(-p2-
p+3)]×2=-2p2+3p+3
∴当p=
时,四边形DEFG的面积取得最大值,
∴D(
,
)、E(
,
).
如答图2所示,过点D关于x轴的对称点D′,则D′(
,-
);

连接D′E,交x轴于点P,PD+PE=PD′+PE=D′E,
由两点之间线段最短可知,此时PD+PE最小.
设直线D′E的解析式为:y=kx+b,
则有
,
解得
∴直线D′E的解析式为:y=
x-
.
令y=0,得x=
,
∴P(
,0).
| 5 |
∴
|
解得
|
∴l:y1=
| 1 |
| 2 |
C′:y2=-x2+4x+1.
∵y2=-x2+4x+1=-(x-2)2+5,
∴ymax=5;
(2)联立y1与y2得:
| 1 |
| 2 |
| 7 |
| 2 |
当x=
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 11 |
| 4 |
∴C(
| 7 |
| 2 |
| 11 |
| 4 |
使y2>y1成立的x的取值范围为0<x<
| 7 |
| 2 |
∴s=1+2+3=6.
代入方程得(1+
| 1 |
| a-1 |
| 3 |
| 6-3 |
解得a=
| 1 |
| 7 |
(3)∵点D、E在直线l:y1=
| 1 |
| 2 |
∴设D(p,
| 1 |
| 2 |
| 1 |
| 2 |
如答图1,过点E作EH⊥DG于点H,则EH=q-p,DH=
| 1 |
| 2 |

在Rt△DEH中,由勾股定理得:EH2+DH2=DE2,即(q-p)2+[
| 1 |
| 2 |
| 5 |
解得q-p=2,即q=p+2.
∴EH=2,E(p+2,
| 1 |
| 2 |
当x=p时,y2=-p2+4p+1,
∴G(p,-p2+4p+1),
∴DG=(-p2+4p+1)-(
| 1 |
| 2 |
| 7 |
| 2 |
当x=p+2时,y2=-(p+2)2+4(p+2)+1=-p2+5,
∴F(p+2,-p2+5),
∴EF=(-p2+5)-(
| 1 |
| 2 |
| 1 |
| 2 |
S四边形DEFG=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
∴当p=
| 3 |
| 4 |
∴D(
| 3 |
| 4 |
| 11 |
| 8 |
| 11 |
| 4 |
| 19 |
| 8 |
如答图2所示,过点D关于x轴的对称点D′,则D′(
| 3 |
| 4 |
| 11 |
| 8 |

连接D′E,交x轴于点P,PD+PE=PD′+PE=D′E,
由两点之间线段最短可知,此时PD+PE最小.
设直线D′E的解析式为:y=kx+b,
则有
|
解得
|
∴直线D′E的解析式为:y=
| 15 |
| 8 |
| 89 |
| 32 |
令y=0,得x=
| 89 |
| 60 |
∴P(
| 89 |
| 60 |
点评:本题是二次函数压轴题,综合考查了二次函数与一次函数的图象与性质、待定系数法、函数最值、分式方程的解、勾股定理、轴对称-最短路线等知识点,涉及考点众多,难度较大.本题难点在于第(3)问,涉及两个最值问题,第1个最值问题利用二次函数解决,第2个最值问题利用几何性质解决.

练习册系列答案
相关题目
已知关于x的一元二次方程x2+ax+b=0有一个非零根-b,则a-b的值为( )
| A、1 | B、-1 | C、0 | D、-2 |
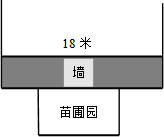 大陇初级中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.如图已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.
大陇初级中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.如图已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.