题目内容
(1+y)2-2x2(1+y2)+x4(1-y)2.
考点:因式分解
专题:
分析:首先补项2x2(1-y2)进而利用完全平方公式以及平方差公式分解因式进而得出答案.
解答:解:原式=(1+y)2+2x2(1-y2)+x4(1-y2)-2x2(1-y2)-2x2(1+y2)
=[1+y+x2(1-y)]2-2x2(1-y2+1+y2)
=(x2-x2y+y+1)2-4x2
=(x2-x2y+y+1+2x)(x2-x2y+y+1-2x)
=[(x2+2x+1)-y(x2-1)][(x2-2x+1)-y(x2-1)]
=[(x+1)2-y(x2-1)][(x-1)2-y(x2-1)]
=(x+1)(x+1-xy+y)(x-1)(x-1-xy-y).
=[1+y+x2(1-y)]2-2x2(1-y2+1+y2)
=(x2-x2y+y+1)2-4x2
=(x2-x2y+y+1+2x)(x2-x2y+y+1-2x)
=[(x2+2x+1)-y(x2-1)][(x2-2x+1)-y(x2-1)]
=[(x+1)2-y(x2-1)][(x-1)2-y(x2-1)]
=(x+1)(x+1-xy+y)(x-1)(x-1-xy-y).
点评:此题主要考查了因式分解法的应用,熟练利用完全平方公式分解因式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.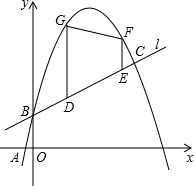 如图,已知一次函数y1=
如图,已知一次函数y1= 如图,已知等边△ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
如图,已知等边△ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.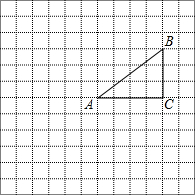 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′. 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)