题目内容
2x4-11x3+22x2-19x+6.
考点:因式分解
专题:
分析:先拆项变形为2x4-11x3+9x2+13x2-19x+6再分组为(2x4-11x3+9x2)+(13x2-19x+6)再运用题公因式法和十字相乘法求解即可.
解答:解:原式=2x4-11x3+9x2+13x2-19x+6,
=(2x4-11x3+9x2)+(13x2-19x+6),
=x2(2x2-11x+9)+(x-1)(13x-6),
=x2(x-1)(2x-9)+(x-1)(13x-6),
=(x-1)[x2(2x-9)+13x-6],
=(x-1)[2x3-9x2+13x-6],
=(x-1)[2x3-2x2-7x2+13x-6],
=(x-1)[2x2(x-1)-(7x2-13x+6)],
=(x-1)[2x2(x-1)-(x-1)(7x-6)],
=(x-1)[(x-1)(2x2-7x+6)],
=(x-1)2(x-2)(2x-3).
=(2x4-11x3+9x2)+(13x2-19x+6),
=x2(2x2-11x+9)+(x-1)(13x-6),
=x2(x-1)(2x-9)+(x-1)(13x-6),
=(x-1)[x2(2x-9)+13x-6],
=(x-1)[2x3-9x2+13x-6],
=(x-1)[2x3-2x2-7x2+13x-6],
=(x-1)[2x2(x-1)-(7x2-13x+6)],
=(x-1)[2x2(x-1)-(x-1)(7x-6)],
=(x-1)[(x-1)(2x2-7x+6)],
=(x-1)2(x-2)(2x-3).
点评:本题考查了拆项法分解因式的运用,分组分解法分解因式的运用,提公因式法分解因式的运用,十字相乘法分解因式的运用,解答时灵活运用各种因式分解的方法是关键.

练习册系列答案
相关题目
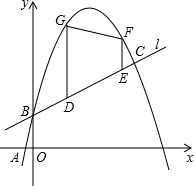 如图,已知一次函数y1=
如图,已知一次函数y1=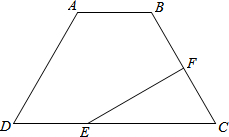 已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF=3,求DC的长.
已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF=3,求DC的长.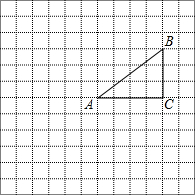 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′. 如图,直线l分别与⊙O1、⊙O2相切于点A、B,AO1=1,BO2=2.⊙O1沿着直线l的方向向右平移,当⊙O1与⊙O2相交时,AB长的范围为
如图,直线l分别与⊙O1、⊙O2相切于点A、B,AO1=1,BO2=2.⊙O1沿着直线l的方向向右平移,当⊙O1与⊙O2相交时,AB长的范围为