题目内容
19.一个多边形的内角和比四边的内角和多540°,并且这个多边形的各个内角相等,这1个多边形的每个内角等于多少度?分析 由题意得出等量关系,即这个多边形的内角和比四边形的内角和多540°,由此列出方程解出边数,进一步可求出它每一个内角的度数.
解答 解:设边数为n,根据题意,得
(n-2)×180°=360°+540°
(n-2)×180°=900°
n-2=5
解得n=7.
900÷7=$\frac{900}{7}$.
答:这个多边形的每一个内角等于$\frac{900}{7}$度.
点评 本题主要考查多边形的内角和定理,解题的关键是由已知等量关系列出方程从而解决问题.

练习册系列答案
相关题目
8.小明同学在计算某n边形的内角和时,不小心多输入一个内角,得到和为2005°,则n等于( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
9.计算(-$\frac{1}{2}$)2016+(-$\frac{1}{2}$)2017得( )
| A. | -$\frac{1}{{2}^{2017}}$ | B. | -$\frac{1}{{2}^{2016}}$ | C. | ($\frac{1}{2}$)2017 | D. | ($\frac{1}{2}$)2016 |
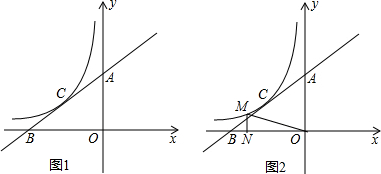
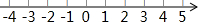
 如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.
如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.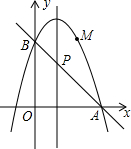 已知二次函数y=-x2+2x+m
已知二次函数y=-x2+2x+m