题目内容
14.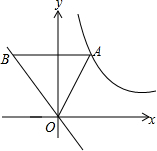 如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.
如图,点A为双曲线y=$\frac{2}{x}$(x>0)的图象上一点,AB∥x轴交直线y=-x于点B.(1)若点B的纵坐标为2,比较线段AB和OB的大小关系;
(2)当点A在双曲线图象上运动时,代数式“AB2-OA2”的值会发生变化吗?请你作出判断,并说明理由.
分析 (1)根据题意求得A、B点的坐标,即可求得AB和OB的长,即可比较线段AB和OB的大小关系;
(2)设A(a,b),则B(-b,b),ab=2.所以利用两点间的距离公式可以求得线段AB、OA的长度;然后可以AB2-OA2的值.
解答 解:(1)∵点B的纵坐标为2,AB∥x轴,
∴A(1,2),B(-2,2),
∴AB=3,OB=2$\sqrt{2}$,
∴AB>OB;
(2)∵直线AB平行于x轴交直线y=$\frac{2}{x}$于点A,
故设A(a,b),
∵A为双曲线y=$\frac{2}{x}$(x>0)上一点,
∴ab=2,
∵B纵坐标为b,
∴B(-b,b)
∴AB2-OA2=(a+b)2-[a2+b2]=2ab=4.
点评 本题考查了反比例函数与一次函数图象上点的坐标特征,勾股定理的应用,利用点A的横坐标表示出点B的坐标是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
5.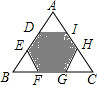 如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
 如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=110°,则∠BCD的度数为125°.
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=110°,则∠BCD的度数为125°.